{2NdV.2_CZ} Nahlížení do Vesmíru. 2
Autoři: geniální předchůdci v mé interpretaci. Sepsal: VVvv. Za konkrétní pomoc jsou poděkováni: profesoři Jiří Bičák a Michal Křížek.
Verze Tenerife – Miraverde, 22. 11. 2021
Tato verze je druhým dílem série článků, který vznikl vyjmutím z původní nulté verze „02NdV1_CZ Nahlížení do Vesmíru, Díl 1“ na samostatnou část. Snahou bylo systematicky docílit etapy, které by popisovaly důsledky použití jednoduchého modelu uzavřeného prostoru s konstantní křivostí k popisu pozorování v prostoru Vesmíru jako celku. A seřadit důsledky od jednodušších k složitějším tak, jak jsem je nacházel na své výpravě do vzdáleného Vesmíru.
K tomuto dílu jsou k dispozici Abstrakt Nahlížení do Vesmíru.2 {2NdV.2A_CZ} a Shrnutí Nahlížení do Vesmíru.2 {2NdV.2S_CZ}.
(Upozornění pro čtenáře: Časové označení závorek mi udává, kdy buď poznámka byla stvořena, nebo přeformulována. Abych si udržel pořádek verzí, změnou textu nebo obrázku změním i datum verze minimálně o jeden den. Slova celá zapsaná velkými písmeny jsou slova ze slovníků, které ale používám ve specifickém významu, který právě upřesňuji svými spisy. Originál spisů je v češtině, mé mateřštině. Dojde-li k nesrovnalostem mezi překlady, má verze v originálu přednost.)
=================================================
2NdV.2_CZ Nahlížení do Vesmíru. 2
A. ÚVOD K DRUHÉ ČÁSTI
B. VÝCHOZÍ BOD
C. ROZPÍNÁNÍ PROSTORU
D. DŮSLEDEK NA NAŠE POZOROVÁNÍ
E. POZOROVÁNÍ PODÉL OBLOUKU
F. GRAVITAČNÍ DEFICIT
< 20210524
V první části Nahlížení do Vesmíru jsme zatím nepotřebovali žádnou fyziku. Představili jsme jenom nejjednodušší geometrický model zakřiveného 3D prostoru, který by mohl vystihnout Einsteinovu myšlenku Vesmíru jako do sebe uzavřeného prostoru, který musí být zakřivený, aby mohl být uzavřený.
Pomohli jsme si uvědoměním, že naše pozorování v 2D prostoru po povrchu koule je stejné jako v 1D prostoru po kružnici, takže sledování přímého směru by nás zavedlo do výchozího bodu z opačné strany. Já jsem jenom tu kružnici nazval jako NÁHRADNÍ KRUŽNICÍ, protože nám nahrazuje přímý směr v prostoru s konstantní křivostí. Měl-li by nás rovný směr zavést zpět do výchozího bodu z opačné strany i v nějakém hypotetickém konstantně zakřiveném 3D prostoru, muselo by i naše pozorování v něm probíhat po NÁHRADNÍCH KRUŽNICÍCH.
Světlo ze zdroje ve skutečném místě „S“ by se potom muselo k nám
pozorovatelům v bodě „P“ šířit po povrchu geometrického útvaru, který jsem nazval „rugball“, jelikož nám svým tvarem připomíná ragbyový míč konstantně zakřivený s vrcholy „P“ a „S“, a který vznikne otáčením NÁHRADNÍ KRUŽNICE kolem spojnice „P-S“, tedy sečny kružnicí. Stále hovoříme jenom o geometrii.
Vesmír ale nemůže být přesně konstantně zakřivený, jelikož to nerovnoměrně rozložená gravitace vylučuje. Tečné směry z „P“ k povrchu „rugball“, které by jinak vytvořily na obloze osvětlenou kružnici, by se zredukovaly na diskrétní směry, podél kterých by se k nám šířilo světlo ze zdánlivých poloh „Z“ na obloze, a které by byly uspořádány do prstence. Průměr takového prstence by se zvětšoval se zvětšující se vzdáleností od nás k pozorovanému zdroji světla „S“, a jeho střed by mířil do skryté pozice „S“.
Kdyby se na obloze podařilo nalézt takové prstence, potom by to už byla fyzika.
20210524 >
< 20210908
6.9. 2021, při své návštěvě pana Jiřího Bičáka, profesora z Ústavu
teoretické fyziky Matematicko-fyzikální fakulty Univerzity Karlovy
v Praze, jsem od něj obdržel upozornění, za které mu děkuji. Tak zvaný gravitational lensing (https://en.wikipedia.org/wiki/Gravitational_lens),
který prý Einstein již předpověděl, se právě potvrzuje intenzivním
studiem Černých děr ve Vesmíru.
Lokální gravitační lensing vzniká
zakřivením prostoru lokální silnou gravitací
Bude-li ověřen první důsledek zvoleného modelu popsaného v první části, potom by to mohlo ukazovat na podobný globální efekt, ale vyvolaný
zakřivením prostoru slabou globální gravitací, která udržuje Vesmír pohromadě.
Modelem předpověděné vícenásobné pozorování objektů ve Vesmíru by nás začalo upozorňovat na možnost, že pozorování předpokládaných unikátních objektů může být pouze optickým efektem našeho pozorování. Mohlo by to být jakési optické zkreslení, které pro přehlednost nazvu jako “První optický klam v nahlížení do Vesmíru”, abych ho odlišil od dalších dvou, které budu probírat právě v tomto druhém dílu.
20210908 >
< 20210522
Podél NÁHRADNÍ KRUŽNICE můžeme od nás pozorovanou vzdálenost vyjádřit jako z=R·φ, kde R je poloměr křivosti prostoru [poloměr NÁHRADNÍ KRUŽNICE] a φ je vzdálenost podél oblouku kružnice měřená v obloukové míře s počátkem v našem bodě pozorování. A rychlost vzdalování (nebo přibližování) pevných bodů na kružnici, pro které jsou φ konstantní, ale jenom poloměr kružnice R se zvětšuje (nebo zmenšuje), se dá zapsat jako časová změna vzdálenosti podél oblouku této kružnice dz/dt= dR/dt·φ, a označením dR/dt symbolem ΔV0, jako ΔV= ΔV0·φ.
Pro popis našeho pozorování se ukázal jako výhodný sférický souřadnicový systém, ve kterém je směr pozorování určen kombinací dvou středových úhlů. Také jsme si uvědomili, že všechna naše pozorování se jakoby promítají do roviny kolmé ke směru pozorování, kterou nazývám ROVINA POZOROVÁNÍ. A jelikož naše pozorování můžeme obecně dělat ve všech různých směrech, můžeme tuto rovinu nahradit tím, co jsme si nazvali BUBLINOU POZOROVÁNÍ, která nás jako pozorovatele kompletně obklopuje.
Náš model nám ale vyloučil představu expandujícího prostoru z nějakého středu expanze do stále vzdálenějšího a více expandovaného prostoru.
V našem modelu totiž není žádné VÝJIMEČNÉ místo, aby v něm mohlo cokoli probíhat jinak, než v ostatních místech. A to musí platit i pro rozšiřování prostoru. Hledání takového procesu, který by nám nějak popisoval rozšiřování prostoru, se nám proto omezí na hledání něčeho, co probíhá ve všech místech stejně.
A právě po tom budeme pátrat v této etapě. A taky jaké důsledky na naše nahlížení do takového prostoru bychom si museli uvědomovat použitím našeho modelu k nahlížení do Vesmíru jako celku.
20210522 >
=================================================
2NdV.2_CZ Nahlížení do Vesmíru. 2
A. ÚVOD K DRUHÉMU DÍLU
B. VÝCHOZÍ BOD
C. ROZPÍNÁNÍ PROSTORU
D. DŮSLEDEK NA NAŠE POZOROVÁNÍ
E. POZOROVÁNÍ PO OBLOUKU
F. GRAVITAČNÍ DEFICIT
< 20170105 V předešlé etapě jsme zkoumali čtyřrozměrný, do sebe uzavřený prostor, který se nám jeví třírozměrný, jako nějaký model matematický, nebo geometrický, chcete-li, abychom zjistili důsledky, které z něho vyplývají. Teď se na naší výpravě dostáváme až k místu, kde budeme zkoumat, zda by takový model mohl být nějak užitečný k modelování pozorování ve skutečném Vesmíru, tak jak se nám jeví.
Pokusíme se zjistit důsledky PŘEDSTAVY, kdybychom použili právě
popisovaný model uzavřeného prostoru s konstantním zakřivením k popisu skutečného prostoru ve Vesmíru. Tedy 4D model, který se nám zevnitř jeví jako 3D prostor a kde pozorované objekty se od pozorovatele vzdalují, a to čím vzdálenější objekty, tím rychleji. Tak, jak nám to Edwin Hubble napovídá objevem červeného posuvu světla, vysílaného z pozorovaných objektů ve Vesmíru.
20170105 >
< 20170105
Každopádně výklad nějakou „expanzí“ prostoru Vesmíru, kde by se něco stále měnícího z méně expandovaného centra s extrémně vysokou hustotou a teplotou hmoty mělo šířit do stále více expandovaného prostoru, takový výklad již není možný. Náš model vyžaduje, aby vše probíhalo ve všech místech stejně včetně rozšiřování prostoru. Tak jakoby něco posunovalo všechno z každého bodu do všech stran, do větší a větší vzdálenosti a současně do větší a větší minulosti v našem pozorování.
Prozkoumat takovou PŘEDSTAVU se jeví jako atraktivní možnost. Tedy aspoň mně, takže jsem nemohl nesledovat takovou stopu. 20170105 >
< 20200804
Ale kdyby se nám taková PŘEDSTAVA náhodou povedla, potom pozor. Nepřestávejme vnímat PŘEDSTAVU jako model, a model zůstane vždycky něco jiného než to, co modeluje.
20200804 >
=================================================
2NdV.2_CZ Nahlížení do Vesmíru. 2
A. ÚVOD K DRUHÉMU DÍLU
B. VÝCHOZÍ BOD
C. ROZPÍNÁNÍ PROSTORU
D. DŮSLEDEK NA NAŠE POZOROVÁNÍ
E. POZOROVÁNÍ PO OBLOUKU
F. GRAVITAČNÍ DEFICIT
< 20200924
Nazvat pozorované vzdalování objektů ve Vesmíru v našem modelu expanzi prostoru, by sice bylo „klasické“, ale nebezpečné, neboť slovo „expanze“ [EN: expansion] sugeruje něco, co má nějaký střed expanze, tedy že taky odněkud vznikla, a že má čelo expanze, tj. kam až expanze dosáhla. Tím sugeruje, že se jedná o nějaký stále se měnící, přechodný [EN: transient] proces, který má svá ohraničení. Ne proces, který by měl být na všech místech průběžně stejný, stejně probíhající, možná až docela ustálený, téměř stacionární (?). A který v důsledku zkreslování našeho pozorování v zakřiveném prostoru se nám jenom jeví jako proces expanze na všechny strany od nás. I když si sami nemyslíme, že zaujímáme nějaké VÝJIMEČNÉ místo ve Vesmíru, které by se právě mělo krýt se středem takové expanze. Proto by bylo lépe volit v češtině nějaké názvy jako „nadýmání“, „bobtnání“, nebo „kypění“, které by lépe vystihovalo takový proces, proces který na všech místech prostoru probíhá stejně. Jinými slovy, aby vystihoval, že naše pozorování takového procesu z jakéhokoli místa našeho pozorování by muselo být stejné, rovnocenné. V každém místě musí probíhat ten stejný proces. Žádné místo v nějakém prostoru, který je do sebe uzavřený s [prostorově] konstantní křivostí, přeci nemůže být nějak VÝJIMEČNÉ, aby v něm mohlo cokoliv probíhat jinak než v ostatních místech? To je přece inherentní tomu modelu
Stále hledám nějaké vhodné české slovo, které by to lépe vystihovalo. Nějaké „nadýmání“ to být nemůže, žádný dým se nevytváří, ani vlhko se nedodává, aby to mohlo být „bobtnání“, a žádná chemická reakce nutná pro „kypění“ se taky nevytváří. A ještě, aby se to slovo mohlo dále snadno používat, mělo by to být dobře přeložitelné do cizích jazyků, snadno i dobře zapamatovatelné, a současně aby nějak vyjadřovalo, že
tento druh rozpínání je jen o trochu něco jiného než dosud používaný název expanze.
S omluvou jsem zatím zvolil pro takový proces lehce zapamatovatelný název (možná trochu s humorem ) EXTÁZE [EN: ecstasy, NL:extase]. V češtině to není daleko od expanze. A kdyby to mělo narazit na velký odpor, tak se klidně znovu omluvím, a odvolám to.
20200901 >
< 20200817
Uznání „expanze“ prostoru ve fyzice si vyžádalo, že zpětnou extrapolací nutně dojdeme k „začátku“ takové expanze, kterou nazýváme „Velký Třesk“ [EN: Big Bang]. Jakýsi singulární bod a singulární okamžik, kde a kdy to všechno „z ničeho“ začalo. Díváme-li se tedy do minulosti, potom ovšem musíme taky narazit na ten konec našeho nahlížení, lépe řečeno na ten začátek, kdy to vše začalo.
Perpetum mobile [EN: Perpetual motion] vylučujeme. Tak nás učí fyzika. A teď najednou tolik energie z ničeho, to by přece byla požehnaně veliká výjimka? (Něco jako známe, že ukradení trochy peněz je taky něco úplně jiného, než ukradení celé banky 😀.)
20200817 >
< 20200917
Jak si ale takový, v každém bodě stejný, proces můžeme představit?
Abychom si mohli udělat aspoň nějakou hmotnější PŘEDSTAVU pozorovaného takového vzdalování, dovolím si nabídnout sugestivní obrázek NÁHRADNÍ KRUŽNICE jako Kruhový Tanec [2NKjKT_CZ]:
V levé části vidíme schematicky jako bychom ty, nebo já, tancovali do kruhu vedle hnědooké Evy a modrookého Adama (s omluvou: jelikož jsem muž, zvolil jsem pro mne atraktivnější místo blíže Evy než Adama 😀) všichni v červeném obleku. Na pravé části se do tance prostorově rovnoměrně přidávají další modře oblečení tanečníci. Z náčrtku je lehce patrné, že Adam se od nás bude vzdalovat rychleji než Eva (a my se budeme od Adama taky vzdalovat rychleji než Eva). Neboli řečeno jinak: Vzdálenější tanečníci se
budou od nás automaticky vzdalovat rychleji než ti bližší, i když jejich úhel φ pozice na kružnici se nezměnil.
Na levé straně je rovněž vyznačen poloměr R kruhu, a taky jak je úhel φ od nás měřen. Na pravé straně je ještě vyznačeno narůstání poloměru kruhu, tedy rozšiřování NÁHRADNÍ KRUŽNICE. Je-li rychlost rozšiřování dR/dt označena symbolem ΔV0, potom pozorovaná rychlost vzdalování podél oblouku má velikost ΔV0 ·φ.
20200917 >
< 20181202
Rozšiřování kruhu tanečníků na našem obrázku připomíná PŘEDSTAVU Hawkinga, prezentovanou v populárně-vědeckém pořadu1 , kde bylo rozpínání Vesmíru zjednodušeně z 3D modelováno do 2D jakoby vzniklé vzájemným „odstrkováním“ objektů do vesmíru.
Bruslaři na ledové ploše byli za sebou seřazeni do tvaru třícípé hvězdy značky Mercedes tak, že se navzájem za sebou opírali a mezi sebou měli připraveny sevřené jakési airbagy. Na povel začali současně nafukovat airbagy, takže expanzí airbagů se začali od sebe odstrkovat, a to tak, že během kontaktu mezi sebou si, čím od středu vzdálenější bruslaři, očividně nabírali větší a větší počáteční rychlost. Potom, když bruslaři ztratili kontakt mezi sebou, pokračovali v pohybu od sebe již pouze setrvačností. Populárně se tak docílila PŘEDSTAVA vesmíru, který vznikl výbuchem nazvaným jako Big Bang.
Bruslaři připomínají náš Kruhový Tanec, ale nejsou stejní. Pohyb bruslařů po ukončení funkce airbagů je uvažován jako setrvačností, kdežto v kruhovém tanci přidávání tanečníků do každého místa probíhá dále. 20181202 >
< 20210601
Tam bylo rozšiřování prostoru vnímáno jako okamžitá aktivita, která skončila výbuchem, a další rozšiřování již pokračuje pouze setrvačností všech objektů, které se výbuchem dostaly do pohybu, a to čím vzdálenější od středu výbuchu, tím rychlejšího. Tedy ne jako nějaké průběžné přidávání tanečníků do NÁHRADNÍ KRUŽNICE, kterou tady reprezentují, a která se plynule a rovnoměrně s plynutím času rozšiřuje.
20210601 >
1 Tato PŘEDSTAVA Stephena Hawkinga je populárně-vědecky prezentovaná v pořadu nazvaném „Genius by Stephen Hawking“ v českém překladu „Genius podle Stephena Hawkinga“
< 20200817
Ale náš model nabízí ještě něco dalšího: Bude-li totiž v našem vyjádření rychlosti vzdalování ΔV= ΔV0·φ ta veličina ΔV0 nenulová (ΔV0 >0), potom s rostoucím φ poroste pozorovaná rychlost vzdalování neomezeně. A pro dostatečnou vzdálenost φ od pozorovatele bude tím pozorovaná rychlost vzdalování dosahovat limitní velikosti ΔV=c, kterou jsem nazval SVĚTELNOU BARIÉROU 2 . Název jsem zvolil podle vzoru „Zvukové bariéry“, která se osvědčila třeba v letectví.
20200817 >
Panem profesorem Bičákem z University Karlovy v Praze jsem byl upozorněn, že tomu, co nazývám SVĚTELNÁ BARIÉRA, by asi nejvíce mohl ve fyzice odpovídat název „kosmologický horizont“. Děkuji mu za toto upozornění.
< 20200807
Přeloženo z https://en.wikipedia.org/wiki/Cosmological_horizon je Kosmologický horizont měřítkem vzdálenosti, ze které by člověk mohl získat informace. Toto pozorovatelné omezení je způsobeno různými vlastnostmi obecné relativity, rozpínajícího se Vesmíru a fyziky kosmologie velkého třesku. Kosmologické horizonty určují velikost a měřítko pozorovatelného Vesmíru. Tento článek dále vysvětluje řadu těchto horizontů (1 Particle horizon, 2 Hubble horizon, 3 Event horizon, 4 Future horizon a 5 Practical horizons).
Jak ale toto měřítko pozorovatelného Vesmíru souvisí s PŘEDSTAVOU velikosti Vesmíru v současné kosmologii? Při hledání odpovědi jsem si otevřel článek https://en.wikipedia.org/wiki/Hubble_volume. (Předem musím upozornit, že otevřením jakéhokoli článku o kosmologii je vidět, jak ohromné množství práce je v ní vykonáno, a kolik našich geniálních předchůdců se podílelo na jejím výzkumu. Proto se asi není co divit, že každý jen trochu laik musí ztrácet přehled, co pro něj kosmologie může vůbec znamenat.)
2 < 20210520 Děkuji panu profesorovi Křížkovi z Matematického Ústavu Akademie věd České republiky za upozornění, jak se již on sám setkal s výpočtem, který uvažoval za „horizontem vesmíru“ větší rychlost pohybu, než je rychlost světla c. Dokonce rychlost převyšovanou až faktorem deset! Prezentovaný model ale nevylučuje PŘEDSTAVU oběhu uzavřeným prostorem po NÁHRADNÍ KRUŽNICI vícekrát opakovaně, a tím i rychlost vzdalování neomezeně narůstající. Takže po prvním oběhu vychází rychlost vzdalování jako ∆V= 2π·∆V0, a každý další oběh k rychlosti přidá zvýšení 2π·∆V0. Potom by bylo možné, aspoň teoreticky, uvažovat i nějakou rychlost třeba o velikosti 10·c. 20210520 >
Zajímavá je prezentovaná vizualizace celého pozorovatelného Vesmíru:
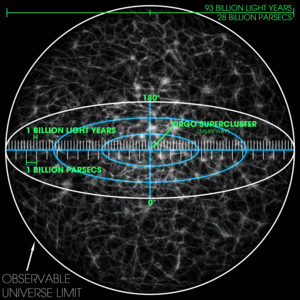
S popisem: Měřítko je takové, že jemná zrnka představují soubory velkého počtu „superklastrů“. „Superklastr Virgo“ – domov Mléčné dráhy – je označen uprostřed, ale je příliš malý na to, aby ho bylo možné vidět
Jelikož my, jako pozorovatelé, bychom pozorovali homogenní Vesmír na všechny strany stejně hluboko, bude naše pozice, naše Země, naše Mléčná dráha samozřejmě zakreslena do středu vizualizace. A to, co nazývám SVĚTELNOU BARIÉROU, je tady nazváno jako Limit pozorovatelného Vesmíru, a je zde znázorněno jako obepínající koule. Ta samá vizualizace je rovněž v https://en.wikipedia.org/wiki/Observable_universe,
s upřesněním, že pozorovatelný Vesmír je sférická oblast Vesmíru zahrnující veškerou hmotu, kterou lze v současnosti pozorovat ze Země nebo z jejích vesmírných dalekohledů a průzkumných sond, protože elektromagnetické záření z těchto objektů mělo čas dosáhnout sluneční soustavy (a Země) od počátku kosmologické expanze. A k té obepínající kouli jsou ještě přidána data, jako je její průměr D=2R≈8,8·1026m, a objem V=π·R3 ·4/3≈3,6·1080m3.
20200807 >
< 20210112
To by ale znamenalo, že je zde myšleno šíření světla k pozorovateli po přímce. Jakoby světlo k nám nepřicházelo podél oblouku, ale podél přímky. Taková přímka je zde použita jako rádius R, aby byl stanoven objem pozorovatelného Vesmíru jako objem koule! To by ale přece nerespektovalo Einsteinovu PŘEDSTAVU, že Vesmír by měl být považován za zakřivený a do sebe uzavřený prostor, kde se světlo musí šířit k pozorovateli podél oblouku? Nerespektuje moderní kosmologie tuto Einsteinovu PŘEDSTAVU?
Pozorujeme-li v zakřiveném prostoru vše po nějakém oblouku, a v prostoru s konstantní křivostí po NÁHRADNÍ KRUŽNICI, potom se ve vzdálenosti odpovídající středovému úhlu 2π (360°) prostorově dostaneme na místo pozorovatele. A dále za ním, bychom začali vše znovu pozorovat, jakoby v „druhém kole“.
20210112 >
=================================================
2NdV.2_CZ Nahlížení do Vesmíru. 2
A. ÚVOD K DRUHÉMU DÍLU
B. VÝCHOZÍ BOD
C. ROZPÍNÁNÍ PROSTORU
D. DŮSLEDEK NA NAŠE POZOROVÁNÍ
E. POZOROVÁNÍ PO OBLOUKU
F. GRAVITAČNÍ DEFICIT
< 20210113
K popisu takových důsledků potřebuji ale nejdříve objasnit několik obecných věcí, abych měl vůbec šanci být pochopen a zabránil tak lavině protestů mých poradců/oponentů. Proč se fyzika brání omezení našeho pozorování? Já sám vidím tu prapříčinu v křečovité snaze, aby se za každou cenu ve fyzice udržela objektivita.
Zřejmě se tím stalo, že my lidé jsme byli vytlačeni z jeviště fyziky a zatlačeni do hlediště. Ano, smíme pozorovat fyziku, a tedy i Vesmír, ale pouze zvnějšku. Byli jsme z Vesmíru „vykopnuti“ ven, a právě s tím se celý život vlastně nedovedu smířit. Zakázali jsme si, aby nás lidé mohli ohrožovat nějak subjektivně ve fyzice. (A možná právem, aby nám ještě i tady začali překážet 😀.)
To naše vyhnanství nás ovšem bude provázet na všech popisech mých
výprav. Dokonce i v základních formách, jako třeba již tady: Jak v tom, co považujeme za objektivní 3D prostor, si vůbec můžeme každý sám dělat navzájem UNIKÁTNÍ subjektivní 2D pozorování toho, co si nazýváme objektivní realita? Nebo obráceně: Jak můžeme z našich individuálních subjektivních 2D pozorování, být vůbec schopni vytvářit si PŘEDSTAVU objektivního 3D prostoru? Jak by to mohlo být možné, když se vše z každého místa vzdaluje odstrkáváním na všechny strany do dálky a taky minulosti, tedy i z místa, kde se nacházíme my?
Tak například od Adama, jako na obrázku BUBLINA POZOROVÁNÍ
v prostru 2 [2BPvp2_CZ], který níže uvedu, by se vše mělo vzdalovat do
vzdálenosti a minulosti od něj, a přitom Eva, která to vše pozoruje třeba z kolmého směru, žádné posouvání od Adama nepozoruje. Nepozoruje vůbec nic. A taky obráceně Adam nepozoruje nic ze vzdalování všeho do vzdálenosti a minulosti od Evy. Jak to, že v takovém prostoru, který od nás ubíhá na všechny strany, můžeme vůbec odpozorovat nějaké 3D geometrické útvary s [matematicky] absolutní přesností?
< 20210115 Ale není se čemu divit. Jelikož v našem modelu je pozorovaná rychlost vzdalování ΔV = ΔV0·φ, potom vyjde matematicky pro nekonečně malé dφ i nekonečně malá rychlost vzdalování dΔV=ΔV0 ·dφ. A fyzikálně, pro neměřitelně malé zakřivení prostoru dφ ≈ 0 musí být i rychlost vzdalování námi nepozorovatelně malá dΔV ≈ 0 (všechny geometrické tvary se stanou absolutně přesné pro limit z= R•φ, když φ → 0). Jinými slovy, v našem bezprostředním okolí, kde zakřivení prostoru není ještě pozorovatelné, tam nemůže být pozorovatelné ani to, co nazývám EXTÁZE.
20210115 >
Aby si ale nikdo nemyslel, že ten důsledek, o kterém se právě chystám
zmínit, byl jen nějaký ojedinělý nápad ráno po nočním divokém snu, tak to ne, právě naopak. Pátral jsem po něm léta. A usilovně.
Jako příklad uvedu třeba týdny intenzivní spolupráce s doktorem
Jósefem Kajfoszem, vědcem z Institutu Jaderné Fyziky v Krakově, na
jednom detailu, jako důsledek jeho odborného článku „On the
alternative interpretation of special relativity“.
Předně mu musím poděkovat za trpělivost v intenzivní konzultaci i
námahu, kterou vložil do naší spolupráce. Ale spolupráce s Kajfoszem mi stála zato. I když jsme vlastně skončili „bouračkou“, kdy můj kolega navrhl skončit další diskusi, neboť jsme dorazili k neprůstřelné, neposuvné „zdi“ ve fyzice zvané jako Twin Paradox. A já jsem ve stejném okamžiku právě zajásal, neboť jsem si konečně uvědomil, že jsme sice narazili na stejnou zeď, ale oba z navzájem opačné strany (!!!!). To mi pomohlo uvědomit si podstatu té zdi natolik, že jsem si ze svých poznámek sestavil pro sebe samostatnou studii nazvanou Pozorování Satelitů a Twin Paradox 20181025 {2PSTP_CZ}, ve snaze ji správně pochopit.
Twin Paradox [https://en.wikipedia.org/wiki/Twin_paradox], jako o čem se jedná, popíšu lidově třeba takto: Představte si, že modrooký Adam by vystřelil hnědookou Evu, ne na Měsíc 😀, ale mnohem dál a rychleji, aby Eva vykonala uzavřenou dráhu Vesmírem a stačila by se nám vrátit nepoškozená zpět. A zatímco byl Adam stále na Zemi, naše Eva procestovala řadu jiných míst, které jsou ve fyzice vnímány jako jisté referenční soustavy [EN: inertial frames. Kajfosz´s terminology: State of Inertial Motion (SIM)], a ve kterých podle současného uznávaného konceptu vychází, že se v nich zpomalil běh času oproti běhu času na Zemi, protože jsou vůči Zemi v pohybu. Tím se nám ale stane, že Eva se vrátí k Adamovi mladší, než je on! A naopak, kdyby Eva zůstala v jedné z těch navštívených referenčních soustav a byl to Adam, který by odletěl od ní na Zem a potom se vrátil k ní, a
cestoval tu stejnou uzavřenou dráhu jako ona, potom by to byl Adam, který by byl mladší než ona! To ovšem normální mozek „nebere“, proto ten název Paradox.
Uvědomte si ale, že se k tomu ve fyzice vychází z jistého fyzikálního
konceptu, z jistého souboru Postulátů, jak se to nazývá, ke kterému jsme se v daném okamžiku až dopracovali gigantickým úsilím velkého počtu geniálních předchůdců.
A s použitím matematických nástrojů, které zase vypracovali a po sobě pro nás zanechali nesčetní geniální předchůdci, můžeme přejít od jednoho konceptu k jinému konceptu, i když jeho důsledky nám někdy třeba nevyjdou.
K tomu všemu si ještě uvědomte, že naše matematické nástroje jsou natolik požehnané, že se na ně můžeme spolehnout ve dne i v noci. Propojují oba koncepty pro nás na tak pevně spojené, s takovou inherentní jistotou, že BUĎ je musíme oba přijmout, NEBO je musíme oba zavrhnout! To je zajištěno tím, že základem všech našich matematických nástrojů je vlastně sčítání, do kterého zahrnuji i násobení, jako opakované sčítání3.
< 20210322
Již tady jsem slyšel hlasy, které mě upozorňují, že zde používám pojmy, jako je „Twin paradox“ a „referenční soustavy“ aniž bych vysvětlil, jak to s vyšetřovaným „Nahlížením do Vesmíru“ vlastně souvisí. To mě přinutilo k vypracování těchto návazných sestřihů svých poznámek, tedy samostatných etap Goulliverovy cesty do říše obrů, do makrosvěta, nazvaných „Nahlížení do Vesmíru“.
20210322 >
A teď už vám prozradím ten důsledek, pro který jsme si vše připravovali.
20210113 >
3 < 20210113 Ale pozor: Jenom takové opakované sčítání, které si můžeme představit třeba jako počítání podlahových dlaždic v obdélníkové místnosti. Tam můžeme přece začít sčítat z jednoho rohu podél jedné stěny všechny dlaždice v řadě za sebou, a potom opakovaně pokračovat přes sousední řady. Anebo podél druhé stěny opakovaně sčítat všechny dlaždice v každém sloupci.
To je ovšem něco jiného než opakované sčítání třeba hlasů voleb amerického prezidenta, kdy by se opakovaným sčítáním mělo dojít ke stejnému součtu volebních hlasů za předpokladu, že se s nimi mezi tím nijak nemanipulovalo. A tím by se i mělo docílit legální volby prezidenta s přesností třeba až jednoho hlasu, ovšem za předpokladu, že všechny hlasy byly získány absolutně legálně a taky legálně sečteny.
K takovým situacím se vrátím ve svých článcích o psychologii, kde nám nastavím zrcadlo, abychom si uvědomili důsledky našeho jednání. Splnění těchto výše uvedených předpokladů může být velice obtížné, pokud se jedná o obrovské osobní VLASTNÍ ZÁJMY. A já k nim ještě přidám SDÍLENÉ ZÁJMY, kde se podílíme na zájmech skupiny lidí, kteří nějak spolupracují, nebo spolupůsobí, nebo se aspoň identifikují s nějakou skupinou (-něco, jako když se začneme identifikovat třeba s Republikány, přestaneme se přece identifikovat s Demokraty, a obráceně-) 20210113 >
< 20200114
Připravili jsme to, abychom se pokusili pokračovat nyní, doufám, že úspěšně. Takže v matematice, která se opírá ve svých základech o jistotu sčítání, musí být 1+1=2 absolutní pravdou (již proto, že jsme si to tak vzájemně dohodli 😀).
Ale pak zároveň musí platit, že 2-1=1! To vyplyne z jedné Okrajové podmínky našeho VĚDOMÉHO MYŠLENÍ, v mé terminologii nazvané třeba jako „BUĎ/NEBO“. A to nám zaviní, že buď přijmeme 1+1=2 a současně 2-1=1, nebo musíme obojí současně zamítnout. Odpovídající důsledky se nám ovšem přijímají nebo vylučují lehčeji v matematice, ve fyzice už to může být podstatně těžší.
Takže teď k věci: Twin Paradox vznikl ve fyzice paralelně se dvěma různými pohledy. Jeden podle PŘEDSTAV, které pro nás vytvořil Albert Einstein, a které vylučují ve Vesmíru existenci jakékoliv VÝJIMEČNÉ referenční soustavy. Všechny soustavy si musí být navzájem rovnocenné, žádná nesmí být VÝJIMEČNÁ.
A ten druhý pohled podle PŘEDSTAV, které pro nás udělal Hendrik Lorentz, ve kterých se vyžaduje, aby pro nás ve Vesmíru existovala aspoň jedna referenční soustava UNIKÁTNÍ tím, že by bylo možno vztahovat k ní naší PŘEDSTAVU relativity.
A právě v naší popisované PŘEDSTAVĚ, v našem modelu, se nám vlastně už podařilo oddělit lokální soustavu, ve které každý z nás subjektivně nahlíží do Vesmíru (viz třeba již prezentovaný obrázek PROSTOR 4D [2P4D_CZ]) od soustavy celého objektivního zakřiveného prostoru s konstantní křivostí.
20200114 >
< 20210113
Pokusím se to ještě zviditelnit pomocí obrázku, který jsem si odvodil z původního obrázku ukazujícího, jak hnědooká Eva a modrooký Adam pozorují jeden a ten samý objekt třeba nějaký klenot, jakoby ve společném bodě svých BUBLIN POZOROVÁNÍ, a který jsem nazval BUBLINA POZOROVÁNÍ v prostoru 2 [2BPvp2_CZ]:
Do obrázku jsem přidal, jak je pro každého pozorovatele pozorování sice UNIKÁTNÍ podle Lorence, ale současně žádné z nich není VÝJIMEČNÉ podle Einsteina. Dali jsme tak vlastně za pravdu oběma. Co jsme tím ale docílili? Odstranili jsme tím Twin Paradox? Ne, vůbec jsme si ho nevytvořili.
20210113 >
Jsem snad jediný, který si nějak všimnul takových důsledků takového
modelu? Důsledků, kdybychom považovali Vesmír za uzavřený
zakřivený prostor? Nebo jsem to já, kdo se doopravdy zbláznil?
Vzpomenu si vždy na jeden fór, který jsem kdysi slyšel: „Babička s dědečkem jedou po dálnici. Babička spustí rádio, kde právě hlásí: Pozor, máme hlášení, že na dálnici mezi místem „A“ a „B“ jede jedno auto v obráceném směru. A dědeček na to: Jak to, jedno auto, všechny auta! “ 😀 .
< 20201008
Ukázali jsme si, že rychlost vzdalování pozorovaná ve Vesmíru je v našem modelu automaticky přímým důsledkem zvětšování vzdálenosti pozorovaných objektů od nás. Rychlost vzdalování je reprezentována narůstáním úhlu φ, ale pouze když ΔV0 se nerovná nule. Kdyby totiž bylo ΔV0=0, potom by k žádnému narůstání vzdálenosti nedocházelo.
Jinými slovy, ΔV0 = dR/dt je rychlost EXTÁZE, kterou musíme brát nenulovou a stejnou v každém bodě pozorovaného prostoru s konstantní křivostí. Potom platí prostorově K = ΔV0 / c = Konstanta > 0. Tedy bezrozměrná konstanta, kde c nám označuje rychlost šíření prostorem například světla (nebo obecně elektromagnetického vlnění), gravitačních rozruchů, změn rozložení energie v prostoru, atd., jako poslední konstantu, když moderní fyzika nám už sebrala Newtonův neměnný běh času i neměnné rozměry prostoru.
< 20210310 Abych se vyhnul opakovanému vyjmenovávání, co vše se v současném konceptu fyziky šíří tou rychlostí c, aniž bych opominul nějaké další, zavedu proto pro ně obecnější název INFORMACE. Volím tento termín, protože ať se něco šíří třeba elektromagnetickým vlněním, nebo gravitačním rozruchem, tak jsou to přece pro nás stále jenom informace o něčem, co pozorujeme, jak se v našem časoprostoru od nás vzdaluje do dálky a současně do minulosti. Doufám, že i v tom najdu pochopení. 20210310 >
Navrhnul jsem nejprve nazvat tuto bezrozměrnou konstantu K = ΔV0 / c jako Kosmologickou Konstantu. Ale s tím jsem u pana profesora Bičáka neuspěl. A dokonce jsem později i zjistil, že tento název se už ve fyzice používá [https://en.wikipedia.org/wiki/Cosmological_constant], takže by
to jenom vedlo k většímu zmatku. Je ale vlastně jedno, jak bychom tu
konstantu nazvali, ovšem nějak by se nazývat měla, abychom na ni
mohli jednoduše a jednoznačně referovat.
Obrázek Náš 1. Postulát [2n1p_CZ] nám konstantu K shrnuje:
Postulát ho nazývám, protože nám matematicky popisuje to samé, co by geometricky mohlo reprezentovat model uzavřeného zakřiveného prostoru s konstantní křivostí, ve kterém pozorujeme, jak se všechny objekty od nás vzdalují. Ta PŘEDSTAVA, ten model, si tu konstantu vyžaduje. Obojí je přece to samé, jen jinak zapsané. Takže BUĎ přijmeme obojí, NEBO musíme zavrhnut obojí. BUĎ přijmeme model i konstantu, NEBO zavrhneme obojí.
Domnívám se ale, že touto dvojicí PŘEDSTAV (které nazývám jako
ZAMĚNITELNÉ PŘEDSTAVY) přece k Einsteinově PŘEDSTAVĚ nic nepřidáváme, ani ji nic neubíráme?
20201008 >
Teď si ještě dovolím zapsat další své „odvozené“ postřehy a důsledky,
které by podle mne mohly vyplývat z již právě popsaných důsledků.
Jsem připraven, že s nimi neuspěji u všech expertů v kosmologii nebo v jiných fyzikálních vědách, takže mi nezbývá než se jim omluvit, kdybych jim kazil náladu nebo je jinak zatěžoval uvažováním nad nimi.
=================================================
2NdV.2_CZ Nahlížení do Vesmíru. 2
A. ÚVOD K DRUHÉMU DÍLU
B. VÝCHOZÍ BOD
C. ROZPÍNÁNÍ PROSTORU
D. DŮSLEDEK NA NAŠE POZOROVÁNÍ
E. POZOROVÁNÍ PO OBLOUKU
F. GRAVITAČNÍ DEFICIT
< 20201013
Naše PŘEDSTAVA nevyžaduje předpoklad nějakého vzniku prostoru Vesmíru z ničeho. A horizont našeho pozorování modeluje jako limit pozorované rychlosti vzdalování předmětů od nás ΔV=c, který nazývám SVĚTELNÁ BARIÉRA. Ten limit vyplyne jako důsledek přirozeného narůstání té pozorované rychlosti ΔV=ΔV0·φ s narůstáním φ, a za kterým limitem již nepozorujeme nic.
20201013 >
< 20201020
Byl to až Stephen Hawking, který mě svými PŘEDSTAVAMI upozornil na omezení vzniklá popisem Vesmíru „klasicky“ jako nějaký otevřený prostor [v Kartézských souřadnicích x-y-z]. Později jsem si uvědomil výhodu brát Vesmír jako uzavřený prostor [pro pozorovatele ho popisovat ve sférických souřadnicích r(≡z=c·t)-φ-ψ se středem v místě pozorovatele].
Naštěstí ani žádnou újmu na objektivitě naším modelem nevytváříme: fyzika zůstává stejná pro jakékoliv místo pozorování, které si můžeme ve své PŘEDSTAVĚ o Vesmíru libovolně měnit.
A jako bonus sférická soustava pozorování se stává pro každého
pozorovatele jedinečná, UNIKÁTNÍ, takže náš model vyhovuje i
PŘEDSTAVĚ Lorentze, aniž by to mohlo překážet objektivní fyzice.
Dokonce si možná můžeme i gratulovat, protože tento model nedal příležitost, aby se mohl vytvořit „Twin Paradox“.
A navíc jsme začali respektovat i skutečnost, na kterou nás Richard
Feynman upozorňuje. Žádní dva pozorovatelé nemohou nikdy současně pozorovat cokoli ze stejného místa pozorování. Hnědooká Eva a modrooký Adam si mohou až láskyplně položit čelo na čelo, nebo líčko na líčko, ale dále ne. V pozorování ze stejného bodu by se museli střídat.
Tak mi tady asi vše jen tak neprojde. Ale dobře, ať to někdo vyvrátí a nabídne lepší PŘEDSTAVU, lepší model. Jsem připraven mu za to děkovat.
„Náš 2. Postulát“ (Náš 2. Postulát [2n2p_CZ]) ovšem znamená, že ve
Vesmíru jako uzavřeném prostoru, ve kterém pozorované objekty jakoby nám od nás ubíhaly na všechny strany rychlostí ΔV, nám model do prostoru „něco“ přidává. A to přidávání je ve všech bodech průběžné, rovnoměrné a stejně rychlé. Kdyby ΔV0 byla konstantní rychlost nejen prostorově, ale dokonce i časově, potom bychom brali rozšiřování NÁHRADNÍCH KRUŽNIC jako stacionární, dR/dt=konstanta, tj. d2R/dt2=0.
A právě pátrání po potom „něčem“, co se nám do prostoru všude
přidává, nás dovede k popisům mých dvou Goulliverových cest do světa trpaslíků, tedy výprav do mikrosvěta, na které vás chci rovněž pozvat. Budeme hledat nějaký most mezi makrosvětem a mikrosvětem, abychom se dopracovali k přesvědčení, že žádný neexistuje. Je jenom jeden Vesmír a ne dva. Uvidíme, že makrosvět a mikrosvět je tentýž Vesmír, pouze v pozorování z jiné strany. Tyto výpravy se ale neobejdou bez důkladné přípravy, která je pro takové cesty nutná. Před tím nám nezbude než popsat základní kameny, na kterých bude naše pátrání stát.
20201020 >
< 20170106
Uvědomme si, že až dosud jsme uvažovali ideální [matematické] prostory, tedy prostory, které jsou nekonečně tenké. Jelikož jedna z podmínek (Psychologické Okrajové Podmínky, {3pop_CZ}) našeho VĚDOMÉHO MYŠLENÍ, kterou si můžeme označit třeba jako „buď ∂ nebo ∆“, nám ale nedovoluje rozdělovat PŘEDSTAVU něčeho, co považujeme za konkrétní a reálné, na něco nekonečně malého („∂“), tedy i prostoru Vesmíru, na něco nekonečně tenkého4 . Populárně se snažím tento fakt vysvětlit ve stati Matematika a Fyzika {0mf_CZ}, ve které táhnu dělicí čáru mezi matematikou a fyzikou.
Proto naši PŘEDSTAVU rozšíříme na prostor konečné tloušťky („∆“)
zavedením pojmu „kvantum délek“ LC, jak popisuji ve stati Kvantum
prostoru, času a energie {2kpce_CZ}. K jakým kvantovým velikostem a k jaké PŘEDSTAVĚ prostoru to vede, rozpracovávám ve stati nazvané
Kvantová DVOJ-VÝMĚNA {2KDV_CZ}.
Jak jsem již upozornil, skutečný prostor Vesmíru nemůže mít konstantní zakřivení, protože zakřivení prostoru vzniká gravitačními účinky, a ty jsou ve Vesmíru nerovnoměrně rozložené. Některé poznámky na toto téma jsem sestavil do samostatné studie, kterou jsem nazval Pozorování Hvězd {2ph_CZ}. Tam si také ukážeme některé důsledky lokálních rozdílů v zakřivení prostoru, které nám deformují NÁHRADNÍ KRUŽNICE na křivky s proměnnou křivostí.
20170106 >
< 20210204
Aniž bych už tady svým popisem vstoupil do diskuze o běhu času, o to se pokouším jinde, potřebuji se tady opřít o následující. Jak upozorňuji jinde:
„Čas jsme si vymysleli, abychom pochopili ZMĚNY“.
V podstatě běh času je jen pevná posloupnost ZMĚN. Populárně řečeno, seřadíme-li si ZMĚNY po sobě do pevného pořadí a očíslujeme-li je, třeba jako 1-2-3-4…, potom pozorováním z libovolného místa se pořadí posloupnosti ZMĚN nezmění. Pozorováním odnikud se nám posloupnost nepřehází, třeba například na posloupnost 1-3-2-4…. I když v pozorování z konkrétního místa můžeme posloupnost takových ZMĚN pozorovat přeházenou.
Jak běží čas v dálce od nás, nebo i jak běžel čas v minulosti, je akademická otázka. Jsme jenom přesvědčeni, že nějak běžel (že nějaké ZMĚNY musely probíhat ve vzdálenosti i v minulosti). Označme si aspoň na chvilku běh času v nějakém místě námi pozorovaném do dálky a současně do minulosti jako τ.
4 < 20170106 Kružnici v matematice můžeme chápat jako nekonečně tenkou. Zakreslená kružnice ale ztratí tuto vlastnost, a nebude již nekonečně tenká. Povrch koule můžeme v matematice považovat za nekonečn
ě tenký. Vytvoříme-li kouli třeba nafouknutím mýdlové bubliny, zase se taková vlastnost ztratí. 20170106 >
Jak to souvisí s modelem Einsteina pro prostor Vesmíru, jako uzavřeného prostoru s konstantní křivostí, ukážeme na dvou jednoduchých případech:
(I) V prvním případě budeme uvažovat vzdalování objektů pozorované
v prostoru, ve kterém je poloměr křivosti R prostorová i časová konstanta. Potom jenom úhel φ oblouku mezi pozorovanými pohybujícími objekty (nebo mezi nimi a námi, pozorovateli) se může měnit s časem (zvětšovat). Pohybující se objekty na povrchu (Země-)koule by byly pozorovány stejně, jako příklad v prostoru o jeden rozměr menším.
V takovém zakřiveném prostoru bychom vzdálenost od nás po oblouku stále chápali jako z=R•φ. A s časovou ZMĚNOU, během které narůstají vzdálenosti od nás k pozorovanému objektu, bude rychlost vzdalování dz/dt= R·dφ/dτ·dτ/dt. Zde t označuje referenční běh času v našem bezprostředním okolí, tedy v naší současnosti, kterou nazýváme přítomnost. A pro zjednodušení, když bychom uvažovali běh času τ a t jako stejný ( dτ /dt=1), potom by byla rychlost vzdalování dz/dt= R·dφ/dt.
My ale takovou ZMĚNU pozorujeme prostřednictvím světla, které se k nám šíří rychlostí c. A my již nemůžeme rozlišit, zda se k nám světlo, které nám přináší informaci o ZMĚNĚ, šířilo po oblouku nebo po přímce. To vedlo k PŘEDSTAVĚ, která svazuje vzdálenost a stáří pozorovaných objektů vztahem z=c·t (nebo dz/dt=c). Takže například objekt vzdálený milión světelných let pozorujeme ve stavu, který měl před miliónem let. A to platí nejen pro všechny vzdálené pozorované objekty, ale i pro vzájemné rozdíly vzdáleností a stáří objektů.
(II) V druhém případě budeme uvažovat vzdalování nehybných objektů unášených EXTÁZÍ rozšiřujícího se prostoru rychlostí ΔV0 prostorově i časově konstantní. Stejně jako pevné objekty, které by se vzdalovaly od sebe na povrchu rovnoměrně se nafukující (Země-)koule, zase jako příklad v prostoru o jeden rozměr menším.
Objekty by zůstávaly na stejném místě, tedy φ by pro ně zůstávalo
konstantní. Pouze by objekty byly unášeny s rozšiřujícím se prostorem. Pro běh času τ a t stejný (dτ/dt=1), zvětšování poloměru křivosti dR/dt = ΔV0 by způsobilo, že narůstání vzájemných vzdáleností Δz=R•Δφ mezi objekty by se nám jevilo jakoby rychlostí dz/dt= dR/dt·Δφ= ΔV0 ·Δφ. Je důležité si uvědomit, že i pro rozpínání zakřiveného prostoru konstantní rychlostí ΔV0 , bude pozorovaná vzdálenost od nás po oblouku z=R•φ a i pozorovaná rychlost vzdalování ΔV= ΔV0•φ narůstat s narůstajícím φ.
A to by stále odpovídalo i našemu pozorování, na které nás upozornil Edwin Hubble. V nezakřiveném prostoru se nám taky jeví, že se nám pozorovaná rychlost vzdalování s rostoucí vzdáleností od nás stále zvětšuje, ale důvod je hledán, v expanzi prostoru s rychlostí, která se stále zvyšuje s růstem vzdálenosti od pozorovatele.
Takže v obou případech pozorujeme stále se zrychlující vzdalování se s
rostoucí vzdáleností od nás. Efekt v nezakřiveném prostoru je vysvětlen tak, jako bychom pozorovali objekty, které se skutečně vzdalují stále se zvyšující rychlostí. Zatímco v zakřiveném prostoru modelujeme ten stejný efekt pouze jako unášení objektů v prostoru, který se rozpíná konstantní rychlostí.
To považuji za podstatný rozdíl a možná i důvod, proč nám vzniká to, co budu níže nazývat jako GRAVITAČNÍ DEFICIT. Pokusím se to ještě plastičtěji prezentovat pomocí náčrtku VĚK a VELIKOST pozorovatelného Vesmíru
[2VVpV_CZ]:
Představme si, že hnědooká Eva a modrooký Adam, jako naši zástupci
v pozorování, pozorují za nás objekty do dálky a minulosti. Eva se soustředí na to, že její pozorování je „klasické“ po přímce, a Adam po oblouku. A je jedno, zdali si Adam vysvětluje, že se k němu světlo šířilo po oblouku v nějakém nezakřiveném prostoru, nebo se k němu šířilo rovně v nějakém zakřiveném prostoru, protože jsou to jenom dvě ZAMĚNITELNÉ PŘEDSTAVY, které vedou k jednomu a tomu stejnému důsledku, k jeho pozorování. Oba se mohou dívat na nejrůznější strany, a ne jenom jako tady, vzájemně obráceným směrem, který volím pro jednoduchost náčrtku. Pořád ale uvidí vzdálenější objekty jako starší, jelikož informace o objektech se k nim nešířila nekonečně velkou rychlostí, ale jenom konečně velkou rychlostí světla c.
Takže v jejich PŘEDSTAVĚ mohou svým VĚDOMÝM MYŠLENÍM vnímat buď stáří objektů t, nebo jejich vzdálenost z, svázané vztahem z=c·t. A když ke svým PŘEDSTAVÁM ještě přidají interpretaci červeného posuvu světla jako rozšiřování Vesmíru, kterým se vzdálenější objekty od nich vzdalují rychlostí, která se stále zvětšuje se vzdáleností od nich, potom dojdou nutně k závěru, že informace, která se k nim šíří nemůže být z míst vzdálenějších než je nějaká limitní vzdálenost. Protože potom by rychlost vzdalování objektů přerostla rychlost světla c.
Tato limitní vzdálenost se ve fyzice nazývá Horizont Vesmíru HV. Je to tedy vzdálenost k limitu pozorovatelného Vesmíru od místa pozorovatele. Z ještě vzdálenějších míst, která by se od nás mohla vzdalovat rychleji než c, by k nám už světlo nedoletělo. Šířilo by se k nám totiž rychlostí c v prostředí, které by se od nás vzdalovalo rychleji než c.
Že já tomu limitu říkám SVĚTELNÁ BARIÉRA, to na věci nic nemění. Stalo se to jenom tím, že jsme k ní došli odlišnou úvahou. Označíme si proto vzdálenost k této bariéře od místa pozorovatele jako SVĚTELNÁ BARIÉRA Vesmíru SBV, takže potom SBV= HV.
Jelikož v naší PŘEDSTAVĚ letělo světlo po celé dráze k nám rychlostí c,
odpovídá těmto vzdálenostem jistý interval běhu času v našem místě
pozorovatele, který si nazveme jako VĚK VESMÍRU VV. Takže potom HV≡SBV= c·VV.
V našem popisu modelu, podle PŘEDSTAVY Einsteina, jako prostoru do
sebe uzavřeného s prostorově konstantní křivostí, můžeme ale interpretovat vzdálenost od nás jako vzdálenost po kruhovém oblouku z= R·φ, ve kterém R opět označuje poloměr kruhového oblouku, a φ označuje odpovídající úhel délky oblouku měřeného ve směru od nás pozorovatelů až k pozorovaným objektům v obloukové míře.
Přidejme si k PŘEDSTAVĚ ještě interpretaci, že pozorovaný červený posuv světla je důsledek EXTÁZE Vesmíru, která unáší časoprostor prostorově konstantní rychlostí ΔV0= dR/dt z každého místa na všechny strany, tedy i ze všech možných míst našeho pozorování. Adam, který EXTÁZI pozoruje po oblouku, vidí narůstající rychlost vzdalování od něj jako dz/dt= dR/dt·φ=ΔV0·φ= ΔV .
V PŘEDSTAVĚ EXTÁZE Vesmíru, můžeme potom nazvat Pozorovanou
VELIKOSTÍ VESMÍRU RPV jako vzdálenost, kam až byl prostor unesen
rychlostí EXTÁZE ΔV0, od nás na všechny strany, za dobu VĚKU VESMÍRU, za časový interval VV. Tím dostaneme RPV= ΔV0 ·VV.
Jelikož převrácenou hodnotu intervalu času nazýváme frekvencí opakování toho intervalu, můžeme si pro úplnost obdobně nazvat převrácenou hodnotu VĚKU VESMÍRU VV. jako FREKVENCI VESMÍRU fV, kde fV= 1/VV= ΔV0 /RPV. Ta určuje, jak frekvenčně EXTÁZE Vesmíru unese časoprostor z každého místa ve Vesmíru až do vzdálenosti rovné VELIKOSTI Pozorovatelného VESMÍRU RPV a do minulosti rovné VĚKU VESMÍRU VV.
Abychom rychlost unášení EXTÁZÍ ΔV0 vyjádřili bezrozměrnou konstantou, zavedli jsme si veličinu K= ΔV0 /c, kde c je rychlost světla s významem, jakou rychlostí se k nám vrací INFORMACE o EXTÁZI zpět z každého místa Vesmíru. Potom K označuje velikost ΔV0 jako frakci rychlosti c.
20210204 >
=================================================
2NdV.2_CZ Nahlížení do Vesmíru. 2
A. ÚVOD K DRUHÉMU DÍLU
B. VÝCHOZÍ BOD
C. ROZPÍNÁNÍ PROSTORU
D. DŮSLEDEK NA NAŠE POZOROVÁNÍ
E. POZOROVÁNÍ PO OBLOUKU
F. GRAVITAČNÍ DEFICIT
Dlouho jsem váhal přidat tuto poslední kapitolu do svého sestřihu
poznámek nazvaného „Nahlížení do Vesmíru 2“, jelikož jsem nevěděl,
jak takový dodatek sepsat. Povzbuzován jsem se rozhodl, že se o to
sepsání nějak pokusím. Nejsem si ale jist, že můj popis bude dostatečný k pochopení následujících možností ověřování modelu, které se mi jeví. Abych předešel eventuální další lavině nedorozumění, nejprve ujasním aspoň svůj směr nahlížení na věc.
< 20201013
V naší PŘEDSTAVĚ modelujeme své pozorování do dálky i do minulosti (!), které probíhá po oblouku zakřivení z=R·φ, a rovněž i modelujeme pozorovanou rychlost vzdalování objektů ΔV=ΔV0·φ. Současná fyzika patrně vychází z PŘEDSTAVY pohledu do dálky, tedy ve směru „expanze“, a PŘEDSTAVU pohledu do minulosti, tedy ve směru proti „expanzi“, musí ignorovat, nerespektuje ji, nebo se k ní přinejmenším obrací zády.
20201013 >
< 20201014
Co je důsledkem? Gravitace mezi vzdálenějšími [ale bohužel ne staršími (!)] objekty musí potom, podle našeho očekávání, slábnout rychleji. Vzdálenosti mezi objekty v nezakřiveném prostoru pozorujeme větší a narůstající rychleji, než jsou v zakřiveném prostoru. Pozorování do dálky odpovídá přeci pozorování po směru expanze v nezakřiveném prostoru, a ta vede k očekávání rychlejšího rozpínání prostoru, než je rozpínání zakřiveného prostoru. (Pro pozorování do minulosti, jako pozorování proti směru takové expanze, by to dokonce vedlo až k očekávanému opaku rozpínání, tedy nějakému smršťování prostoru). Očekávané rychlejší rozpínání prostoru ve fyzice musí ale vést i k očekávání rychlejšího slábnutí gravitace. Tedy to vede k očekávání, které se v našem pozorování nepotvrzuje. Naopak, naše pozorování nás mohou upozorňovat, jakoby ve vzdáleném Vesmíru nějaká gravitace chyběla. Takže nám asi nezbývá než za chybějící gravitaci si nějakou gravitaci dosadit. Což možná už uděláme, pomocí třeba tak zvané „temné hmoty“?
20201014 >
< 20210202
Teď ale musím pojmenování zvolit. Buď GRAVITAČNÍ DEFICIT [EN: GRAVITY DEFICIT], nebo DEFICIT GRAVITACE [EN: DEFICIT of GRAVITY]? Dejme tomu, zvolím to první.
Myšlenku GRAVITAČNÍHO DEFICITU si popíšeme hrubě pomocí náčrtku nazvaného GRAVITAČNÍ DEFICIT [2GD_CZ]:
Skutečný vztah mezi pozorovaným červeným posuvem světla, tedy rychlosti vzdalování pozorovaných objektů, a GRAVITAČNÍM DEFICITEM ponechám raději odborníkům.
Na náčrtku je zakreslen rychlostní diagram, kde je na svislé ose vynášena rychlost vzdalování, a na vodorovné ose běh času do minulosti a vzdálenosti:
- na horním okraji je čas vzdalování objektů od nás t´, a v jiném měřítku
- na dolním okraji je čas letu světla od objektů k nám nazpět t.
My, jako pozorovatelé v bodě O, pozorujeme objekty, jak se od nás vzdalují. Rychlost vzdalování objektů „v“ i jejich vzdálenost „z“ (a odpovídající stáří z/c) jsou určovány z pozorovaného červeného posuvu dopadajícího světla, které se šíří zpět z objektů k nám pozorovatelům rychlosti c.
V našem popisovaném modelu pro prostorově konstantní zakřivení se prostor rozšiřuje EXTÁZÍ všemi směry od pozorovatelů stejnou rychlostí ΔV0≡ dR/dt <c, kde ΔV0 je prostorová konstanta.
Uvážíme-li EXTÁZI jako nějaký stacionární proces, potom se stane ΔV0 i časovou konstantou. Jelikož pro pozorovatelný Vesmír jsme si již jeho stáří označili jako VĚK VESMÍRU t=Vv, potom pro unášivou rychlost EXTÁZE ΔV0 bude Pozorovatelná VELIKOST VESMÍRU RPv=ΔV0•Vv, která v náčrtku odpovídá ploše obdélníku o vrcholech D-E-I-O.
Jelikož rychlost vzdalování ΔV0 je frakce K rychlosti světla c, (K=ΔV0/c), potom bude čas letu světla zpět t ve stejném poměru kratší než čas potřebný ke vzdálení objektů t´ (t= t´•K). Na náčrtku odpovídá tomu poměru K poměr ploch obdélníků D-E-I-O a D-K-N-O, nebo poměr úseček I-O a N-O, a samozřejmě i D-E a D-K.
Jelikož ale pozorujeme objekty v zakřiveném prostoru po kruhovém oblouku, potom nejvzdálenější pozorovaný objekt nemůže nikdy ležet dál, než na opačné straně kružnice, tedy od pozorovatele ve vzdálenosti φ=π. Protože jakýkoli pozorovaný objekt pro φ>π by byl již vlastně pozorován v opačném směru pro φ<π. Takový objekt nemůžeme ale započítávat do Vesmíru dvakrát, protože ve Vesmíru ani dvakrát nemůže být. Abychom nezapočítávali prostor Vesmíru v „druhém kole“, potom vychází „skutečná“ VELIKOST VESMÍRU jako Rv= R·π, která na náčrtku odpovídá jenom modře vyznačené ploše obdélníku C-F-I-O.
Uvážíme-li zjednodušeně rychlost pozorovaného vzdalování objektů v jako lineárně závislou na jejich stáří t a současně na jejich vzdálenosti z= c·t (například pro dvojnásobně vzdálený a tedy i dvojnásobně starý objekt je i jeho rychlost vzdalováni dvojnásobná), potom můžeme narůstající rychlost vyjádřit v náčrtku diagonálou v= c·t/Vv, vedenou body O-H-J-K. Je to proto, že času t rovnému VĚKU VESMÍRU t=Vv odpovídá právě rychlosti vzdalování v=c. A bude-li se po celou dobu Vv světlo šířit k nám konstantní rychlostí c, potom bude pro Horizont Vesmíru Hv a SVĚTELNOU BARIÉRU Vesmíru SBv platit Hv≡ SBv= c·Vv, odpovídající na náčrtku ploše celého obdélníku D-K-N-O.
Takže rychlost v na náčrtku roste lineárně s během času (ve vztahu v= c·t/Vv jsou c a Vv konstanty), na náčrtku je rychlost vyznačená diagonálou. A rychlost ΔV0 vzdalování EXTÁZÍ v modelu zakřiveného prostoru bereme jako konstantní, na náčrtku vyznačenou modrou vodorovnou úsečkou E-F-G-H-I. Jelikož plochy vyšrafovaných trojúhelníků A-H-O a G-H-J (a tedy i rovněž symetrického trojúhelníku H-I-O) jsou stejné, bude vzdálenost v bodech G a J pro oba modely stejná. Ta vzdálenost pro model zakřiveného prostoru bude odpovídat ploše obdélníku B-G-I-O, a pro model nezakřiveného prostoru bude odpovídat stejně velké ploše trojúhelníku B-J-O.
Až do bodu H zůstávalo vzdalování v nezakřiveném modelu pozadu, ale v bodech G a J se nám vzdálenosti vyrovnaly. A potom pro místa vzdálenější nám vzdálenost v nezakřiveném prostoru bude stále rychleji narůstat než v zakřiveném prostoru.
Soustřeďme se teď pouze na vzdálenosti mezi pozorovanými objekty.
Vzdálenosti mezi objekty v modelu zakřiveného prostoru budeme označovat modře a podtržené Δz, zatím co v modelu nezakřiveném černě Δz. Potom pro objekty vzdálenější než v bodech G a J, je vzdálenost mezi objekty pro nezakřivený prostor nejen větší Δz>Δz, ale bude i stále rychleji narůstat.
To nám ale způsobí, že pro větší vzdálenost od nás bude vzdálenost mezi objekty Δz nejen větší, ale také očekávaná gravitace mezi nimi bude slabší, než by odpovídalo vzdálenosti Δz v zakřiveném prostoru, jelikož intenzita gravitace klesá podle PŘEDSTAVY Newtona s druhou mocninou vzdálenosti. A ve chvíli, kdy očekávaná oslabená gravitace přestane odpovídat našemu pozorování, začneme si uvědomovat, že nám vlastně nějaká gravitace ve vzdáleném Vesmíru chybí. Tuto skutečnost jsem nazval GRAVITAČNÍM DEFICITEM.
To možná vedlo k očekávání nějaké nepozorovatelné hmoty, která svou gravitací doplňuje chybějící gravitaci, a kterou nejsme schopni přímo pozorovat, ani její pohyb a setrvačné účinky, pouze její gravitační účinky. A protože tuto hmotu považujeme za neviditelnou, dostala název „temná hmota“ [EN: dark matter] https://en.wikipedia.org/wiki/Dark_matter:
„Dark matter is a form of matter thought to account for approximately 85% of the matter in the universe and about a quarter of its total mass–energy density or about 2.241×10−27 kg/m3. Its presence is implied in a variety of astrophysical observations, including gravitational effects that cannot be explained by accepted theories of
gravity unless more matter is present than can be seen“.
A v překladu:
„Temná hmota je forma hmoty, o níž se předpokládá, že tvoří přibližně 85% hmoty ve vesmíru a asi čtvrtinu jeho celkové hustoty hmoty energie neboli asi 2.241×10–27 kg/m3. Její přítomnost je implikována v různých astrofyzikálních pozorováních, včetně gravitačních efektů, které nelze vysvětlit přijatými teoriemi gravitace, pokud není přítomno více hmoty, než je možné vidět.“
To ale otevírá možnost, že popsaným Einsteinovým modelem zakřiveného prostoru by příčina GRAVITAČNÍHO DEFICITU, jako očekávaná „temná hmota“, mohla být nahrazena EXTÁZI prostoru s prostorovou konstantou ΔV0. Jinými slovy možnost, že i velikost prostorové konstanty ΔV0 by se dala nějak stanovit z posuvu červeného světla tak, aby se tím „chybějící“ gravitace doplnila a odstranila nutnost zavádění „temné hmoty“. To by ovšem byl úkol a
úsilí pro nějaké odborníky, kterým já ale nemohu nijak konkurovat. Takže druhá možnost ověření spočívá v:
(2) Nastavení parametrů modelu tak, až by
model odstranil GRAVITAČNÍ DEFICIT.
20210202 >
< 20211116
Problém GRAVITAČNÍHO DEFICITU se ještě pokusím zviditelnit pomocí obrázku HVĚZDY A ŠÍŘENÍ SVĚTLA G [2phG_CZ] z první části tohoto spisu. Tam ukazuji 3 náčrtky, které si ale jejich spojením přepracujeme do jednoho, jak ukazuje obrázek Zkreslení pozorovaných Vzdáleností [2ZpV_CZ]:
Obrázek ukazuje, jak světlo z nejvzdálenějšího zdroje světla v bodě „S3“ se šíří k nám pozorovatelům v místě „P“ podél sytě vyznačené NÁHRADNÍ KRUŽNICE tak, že ho pozorujeme, jakoby dopadalo k nám ze zdánlivé pozice „Z3“, odkloněné od spojnice P-S3 o maximální úhel 90°. A světlo z bližšího zdroje „S2“ pozorujeme, jak se šíří podél světleji zakreslených NÁHRADNÍCH KRUŽNIC, jakoby dopadalo ze zdánlivé pozice „Z2“ odkloněné, pro tuto situaci, úhlem 45°.
Situaci si ale zjednodušíme tím, že budeme uvažovat o hvězdách „S1“, „S2“ a „S3“ (z náčrtků 1 až 3), jakoby existovaly současně. Proto na chvíli zastavíme běh času, a tím zmrazíme jejich pozice v časoprostoru. Přestože třeba světlo z S2 letělo k nám pozorovatelům v bodě „P“ po oblouku vzdáleností L2=R·π/2 a z S3 dvojnásobnou vzdáleností L3=R·π (R je poloměr zakřivení prostoru), tak tím vlastně pozorujeme hvězdu S3 v dvojnásobné minulosti než hvězdu S2. Zmrazením chodu času budeme ale jejich pozice brát v prostoru jako neměnné.
Od pozorovatele v bodě P je hvězda S2 vzdálena V2=R·√2 a hvězda S3
V3=2·R, tím vychází jejich skutečná modře vyznačená vzájemná vzdálenost V23=(2-√2)·R ≈0,5858·R. My, jako pozorovatelé v P, ale pozorujeme hvězdu S2 v její zdánlivé poloze Z2 od nás ve vzdálenosti L2=R·π/2 ve směru 45° odkloněného od spojnice P-S2. A hvězdu S3 pozorujeme v její zdánlivé pozici Z3 od nás ve vzdálenosti L3=R·π ve směru 90° odkloněného od stejné spojnice. Jejich vzájemný úhel v našem pozorování bude proto 45°, jak vyznačeno na obrázku.
Podle kosinové věty, čtverec jejich vzájemné vzdálenosti, námi pozorované, je L232=L22+L32-2·L2·L3·cos45°=R2·π2·(5/4-1/√2)≈ 5,35814·R2, a jejich pozorovaná vzdálenost L23≈ 2,3148·R oproti skutečné vzdálenosti V23≈0,5858·R, takže L23/V23≈ 3,95. Zkreslená vzdálenost L23 je téměř čtyřikrát větší (!) než skutečná vzdálenost V23, a tím i odpovídající vzájemný gravitační účinek by vyšel, pro tuto situaci, téměř šestnáctkrát slabší (!!).
Uvážíme-li, že hvězda S1 je od nás blízko (L1≈V1≈0), takže vliv zakřivení
prostoru na její pozorování je ještě zanedbatelný, potom můžeme obdobně vyčíslit odpovídající zkreslení pozorované L12 (=L2) a skutečné V12 (=V2) vzdálenosti mezi S1 a S2, blíže k nám pozorovatelům, jako L12≡L2= R·π/2≈ 1,5708·R a V12≡V2= R·√2≈ 1,4142·R, takže L12/V12≈ 1,11. Zkreslením se pozorovaná vzdálenost taky zvětšila, ovšem jen nepatrně o přibližně 11% oproti skutečné vzdálenosti.
Přestože jsme si, jenom pro jednoduchost, zvolili zvláštní symetrický případ pozorování objektů od nás v přímce za sebou, a pro zmražení běhu času, omezujeme platnost na jejich vzájemné vzdálenosti podstatně menší, než je poloměr zakřivení prostoru, a na rychlost jejich změn polohy v prostoru podstatně menší než je rychlost světla, ukázali jsme si, jak model předpovídá zesilující efekt zvětšení vzájemných vzdáleností pozorovaných objektů s jejich zvětšující se vzdáleností od nás.
Uvažujeme-li tak veliká zkreslení vzájemných vzdáleností pozorovaných objektů ve vzdáleném Vesmíru, jak předpovídá popsaný model, nevyhneme se uvažování o velkém GRAVITAČNÍM DEFICITU mezi nimi.
To by mohlo poukazovat na dosud mylně interpretovaný efekt zakřivení, který možná vyžadoval, aby se zavedla tak zvaná temná hmota, která by svou gravitací kompenzovala chybějící gravitaci. Tedy nějaká neviditelná hmota, o které se předpokládá, že představuje přibližně 85% hmoty ve Vesmíru. Tedy tak veliké množství, že na pozorovatelnou „světlou hmotu“ by ve Vesmíru už zbývalo jenom pouhých zbylých 15% (!!!).
V mých konzultacích s experty ve fyzice jsem byl ujišťován, jak jsou všichni
přesvědčeni o správnosti tak zvané Einsteinovy rovnice pole (EN:
Einstein field equation a taky odpovídajících Friedmannových rovnic
https://en.wikipedia.org/wiki/Friedmann_equations), která vyplynula
z velkého počtu úspěšných aplikací. Proč ale jejich výsledky začaly vyžadovat temnou hmotu?
I když jsem sám nucen přijmout, že tyto rovnice správně popisují uvažované situace, ale dost možná, že jenom správně popisují špatně modelované situace. Tedy situace, které nedostatečně modelují zakřivení prostoru?
20211116 >
To by ovšem byla, pro mnoho lidí včetně mě, jiná nečekaná situace.
Důvod, proč jsem po konzultacích s profesorem Křížkem, popis prvních 3 důsledků mnou zvoleného modelu “Nahlížení do Vesmíru” rozdělil na dvě části. I když sice všechny důsledky připomínají optická zkreslení a já je nazývám jako první, druhý a třetí optický klam v nahlížení do Vesmíru, jejich eventuální akceptace může probíhat zcela různě.
První optické zkreslení nám způsobuje, že se můžeme mýlit, když si myslíme, že v každém směru pozorujeme unikátní vesmírný objekt, ale mohou to být pozorování jen jednoho a toho samého objektu, v různých směrech, podle modelu seskupených do prstence na obloze, který zvětšuje svůj diametr se vzdáleností k pozorovanému objektu. To může být nečekané, ale nemuselo by to vyvolávat žádný velký osobní odpor.
Ale to třetí optické zkreslení, kterému říkám GRAVITAČNÍ DEFICIT, je
něco jiného. Dovedu si představit, že někoho, kdo celý život nebo
velkou část své profesionální kariéry pátral po temné hmotě, nemusí s nadšením slyšet, že by to mohlo být jenom nějaké optické zkreslení,
které drze nazývám optický klam! To může bolet, a takového člověka
bych nechtěl ranit.
< 20211112
Závěrem můžeme shrnout, že popisovaný model předpovídá to, co je obsahem prvního dílu a co nazývám „První optický klam nahlížení do Vesmíru“. Ten nám připomíná „Local Gravitational Lensing“, známý důsledek silné lokální gravitace, takže bychom si ho mohli nazývat jako „Global Gravitational Lensing“, který by mohl být důsledkem slabé globální gravitace, která drží Vesmír pohromadě.
Popsali jsme si ale i další dva možné optické klamy. Druhý, který vysvětluje progresivně se zvětšující červený posuv světla ze vzdálenějších galaxií, jako optické zkreslení inherentně zaviněné pozorováním v zakřiveném prostoru, který se ve všech místech rozšiřuje stejně, efektem, který nazývám jako EXTÁZE prostoru.
Třetí optický klam nahlížení do Vesmíru je založen na zjištění, že vzdálenosti mezi odlehlými objekty jsou v modelu zakřiveného do sebe uzavřeného prostoru podstatně menší než v otevřeném prostoru. Znamenalo by to, že současná fyzika možná správně počítá pozorovanou situaci ale ve špatně modelovaném zakřiveném prostoru, a tím vypočítává GRAVITAČNÍ DEFICIT ve vzdáleném Vesmíru a potřebu ho kompenzovat tak zvanou temnou hmotou.
20211112 >
< 20211119
Uvědomme si ale, že gravitační pole Mléčné dráhy ovlivňuje takováto pozorování, která by mohla být snadněji proveditelná někým vně galaxie. My ale nežijeme ani mimo galaxii, ani uprostřed ní.
Dráha, kterou by se jinak světlo šířilo k nám po povrchu útvaru „rugball“, musí být v různých směrech různě dodatečně deformovaná. Takové ovlivnění, takové zkreslení, by mohlo být nejmenší pro osu „rugballu“ ve směru paralelním s osou rotace galaxie, nebo ve směru spojnice naší polohy se středem galaxie. Gravitační čočka by mohla být pro nás, v takových směrech „lépe vybroušená“, než v ostatních směrech.
Kompenzace pozorování ovlivněného zkreslením gravitačním polem Mléčné dráhy, by mohl být složitý úkol. Na druhou stranu, očekávaný vliv na pozorování GRAVITAČNÍHO DEFICITU zevnitř galaxie, by mohl být menší. Jde tady o pozorování v nepatrném zorném úhlu, takže i očekávané vzájemné rozdíly v dráze světla by mohly být menší. 20211119 >
Tímto jsem skončil popis druhého dílu, druhé etapy na cestě pátrání nazvané Nahlížení do Vesmíru. V příštích etapách budu prezentovat sestřih svých poznámek, abych jím popsal další důsledky použití modelu uzavřeného prostoru s konstantní křivostí k hrubému popisu prostoru Vesmíru, jako celku.
Ve třetí části jsou uvedeny důsledky širšího chápání takto modelovaného časoprostoru, a ve čtvrté části je vypracováno porovnání důsledků modelu uzavřeného a otevřeného prostoru.
< 20210330
Poděkování
Děkuji všem geniálním předchůdcům, autorům tohoto spisu, kteří mi dali příležitost pokusit se shrnout a interpretovat některé jejich výsledky. Rovněž bych chtěl poděkovat všem členům své rodiny, kteří moje spisování snášeli, a někdy i přispívali k jeho formulování.
Dále děkuji všem ostatním, kteří se na mém spisování podíleli. Kromě řady nejmenovaných jsou to:
- Profesor Jiří Bičák, za jeho vytrvalost usměrňovat moje myšlenky.
- Profesor Michal Křížek, za jeho cenné informace a posouzení.
- RNDr Jósef Kajfosz, který mi pomohl objasnit rozdíly Einstein – Lorentz.
- RNDr Jiří Kopecký CSc, který mě s ním seznámil, a ve spisování povzbuzoval.
- Inženýři Jan Kašpar a Jan Sláma, kteří mě učili vyjadřovat se populárně.
- Překladatelka Libuše van Dijk – Lisová, která dohlédla na mou češtinu.
- Pan Martin Orešanský z Royalonogy, který převádí články na webový formát WordPress.
A nakonec bych ještě rád poděkoval i tobě, vážený čtenáři, za tvoji pozornost, kterou jsi mi věnoval přečtením tohoto druhého dílu. Děkuji.
20210330 >
