2NdV.2_EN Looking into Universe. 2
Authors: brilliant predecessors in my interpretation. Composed by VVvv. Translated by Google translate, ran by VVvv. Thanks are given to professors Jiri Bicak and Michal Krizek.
Version Tenerife – Miraverde, November 22, 2021
Translated October 9, 2022
This version is the second part of a series of articles, which was created by extracting from the original zero version “02NdV1_EN Looking into Universe, Part 1” into a separate part. The effort was to systematically reach stages that would describe the consequences of using a simple model of closed space with constant curvature to describe observations
in the space of the Universe as a whole. And order the consequences from simpler to more complex as I found them on my expedition to the distant Universe.
The Abstract Looking into Universe.2 {2NdV.2A_EN} and Summary Looking into Universe.2 {2NdV.2S_EN} are available for this work.
(Notice to reader: The timestamp of the parentheses tells me when the note was either created or reformulated. To keep the versions organized, if I change the text or image then I change the date of version by at least one day. The whole words written in capital letters are words from dictionaries, which I use in a specific meaning, and which I am specifying in my writings. The original files are in Czech, my mother language. If there are discrepancies between the translations, the version in the original takes precedence.)
=================================================
2NdV.2_EN Looking into Universe. 2
A. INTRODUCTION TO PART TWO
B. STARTING POINT
C. EXPANSION OF SPACE
D. IMPLICATION ON OUR OBSERVATIONS
E. OBSERVATION ALONG THE ARC
F. GRAVITY DEFICIT
< 20210524
In the first part of Looking into the Universe, we didn’t need any physics yet. We presented only the simplest geometric model of a curved 3D space that could capture Einstein’s idea of the Universe as a self-contained space that must be curved in order to be closed.
We helped us by realizing that our observation in 2D space along the surface of a sphere is the same as in 1D space along a circle, so following a straight line would take us to the starting point from the opposite side. I just called that circle a SUBSTITUTIVE CIRCLE because it substitutes a straight direction in space with constant curvature. If a straight direction were to lead us back to the starting point from the opposite side even in some hypothetical constantly curved 3D space, our observation in it would also have to take place along SUBSTITUTIVE CIRCLES.
The light from the source at the actual location “S” would then have to travel to us observers at the point “P” along the surface of a geometrical figure which I have called “rugball” because its shape reminds us of a rugby ball constantly curved with the vertices “P” and ” S”, and which is created by turning the SUBSTITUTIVE CIRCLE around the connecting line “P-S”, i.e. the secant of the circle. We are still only talking about geometry.
If such a model could be applied to our looking into the Universe, then it would begin to be physics.
But the universe cannot be exactly constantly curved, since unevenly distributed gravity precludes this. Tangential directions from “P” to the “rugball” surface, which would otherwise form an illuminated circle in the sky, would be reduced to discrete directions along which light would travel to us from apparent “Z” positions in the sky, and which would be arranged into a ring. The diameter of such a ring would increase with increasing distance from us to the observed light source “S”, and its center would point to the hidden position “S”.
If such rings could be found in the sky, then it would already be physics.
20210524 >
< 20210908
On September 6, 2021, during my visit to Mr. Jiri Bicak, professor from the Institute of Theoretical Physics, Faculty of Mathematics and Physics, Charles University in Prague, I received a notice from him, for which I thank him. The so-called gravitational lensing (https://en.wikipedia.org/wiki/Gravitational_lens), which is said to have been predicted already by Einstein, is currently being confirmed by an intensive study of black holes in the Universe.
Local gravitational lensing occurs by the
curvature of space due to local strong gravity.
If the first consequence of the chosen model described in the first part is verified, then it could point to a similar global effect but caused by the
curvature of space due to weak global gravity that holds the Universe together.
The model-predicted multiple observations of objects in the Universe would begin to alert us to the possibility that observing of assumed unique objects may be just an optical effect of our observation. It could be some a kind of optical distortion, which for clarity I will call “The First Optical illusion in looking into the Universe”, to distinguish it from the other two, which I will be discuss in this second part.
20210908 >
< 20210522
Along the SUBSTITUTIVE CIRCLE, we can express the observed distance from us as z=R•φ, where R is the radius of curvature of the space [radius of the SUBSTITUTIVE CIRCLE] and φ is the distance along the arc of the circle measured in arc measure with the origin at our point of observation. And the speed of moving away (or moving closer) of fixed points on the circle, for which φ is constant but only the radius of the circle R increases (or decreases), we can then write as the time change of the distance along the arc of this circle dz/dt= dR/dt•φ, and by marking dR/dt with the symbol ΔV0, as ΔV= ΔV0 •φ.
A spherical coordinate system, in which the direction of observation is determined by the combination of two central angles, has proven to be advantageous for describing our observation. We also realized that all our observations seem to be projected onto a plane perpendicular to the direction of observation, which I call the PLANE OF OBSERVATION. And since we can generally do our observations in all different directions, we can replace this plane with what we call the OBSERVATION BUBBLE, which completely surrounds us as observers.
But our model ruled out the idea of an expanding space from some center of expansion to an increasingly distant and more expanded space. There is no EXCEPTIONAL place in our model where anything can happen differently than in other places. And this must also apply to expanding the space. The search for such a process, which would somehow describe the expansion of space, is therefore limited to the search for something that takes place in all places in the same way.
And that is exactly what we will be looking for in this stage. And also what consequences we would have to be aware of when looking into such a space by using our model to look into the Universe as a whole.
20210522 >
=================================================
2NdV.2_EN Looking into Universe. 2
A. INTRODUCTION TO PART TWO
B. STARTING POINT
C. EXPANSION OF SPACE
D. IMPLICATION ON OUR OBSERVATIONS
E. OBSERVATION ALONG THE ARC
F. GRAVITY DEFICIT
< 20170105
In the previous stage, we examined a four-dimensional self-contained space, which appears to us to be three-dimensional, like some kind of mathematical or geometric model, if you like, in order to find out the consequences that follow from it. Now we are getting to the point on our journey where we are going to investigate whether such a model might be useful in modeling observations in the real Universe as it appears to us.
We will try to see the consequences of the IDEA if we were to use the constant curvature closed space model just described to describe the actual space in the Universe. That is, a 4D model that appears to us as a 3D space from the inside and where the observed objects move away from the observer, and the farther the objects, the faster. As Edwin Hubble tells us with the discovery of the red shift of light emitted from observed objects in the Universe.
20170105 >
< 20170105
In any case, the interpretation of some “expansion” of the space of the Universe, where something constantly changing from a less expanded center with an extremely high density and temperature of matter should spread into an increasingly expanded space, such an interpretation is no longer possible. Our model requires that everything happens equally in all places, including the expansion of space. It is as if something is pushing everything from every point in every direction, to a greater and greater distance, and at the same time to a greater and greater past in our observation.
Exploring such an IDEA seems like an attractive possibility. Well, at least to me, so I couldn’t help but follow such a trail.
20170105 >
< 20200804
But if such an IDEA happens to be successful, then watch out. Let’s not stop perceiving the IDEA as a model, and the model will always remain something other than what it models. 20200804 >
=================================================
2NdV.2_EN Looking into Universe. 2
A. INTRODUCTION TO PART TWO
B. STARTING POINT
C. EXPANSION OF SPACE
D. IMPLICATION ON OUR OBSERVATIONS
E. OBSERVATION ALONG THE ARC
F. GRAVITY DEFICIT
< 20200924
To call the observed receding of objects in the Universe in our model the expansion of space would be “classical”, but dangerous, because the word “expansion” suggests something that has some center of expansion, i.e. that it also originated from somewhere, and that it has the front of the expansion, i.e. how far the expansion has reached. This suggests that it is some sort of ever-changing transient process that has its boundaries. Not a process that should be continuously the same in all places, equally ongoing, perhaps quite stable, almost stationary (?). And which, due to the distortion of our observation in curved space, only appears to us as a process of expansion in all directions from us. Although we ourselves do not think that we occupy some EXCEPTIONAL place in the Universe that should coincide with the center of such an expansion.
Therefore, it would be better to choose some names in English such as “flatulence“, “swelling“, or “effervescence” [CZ original: „nadýmání“, „bobtnání“, „kypění], which would better describe such a process, a process that takes place in the same way in all places of space. In other words, it would capture that our observation of such a process from any point of our observation would have to be the same, equivalent. The same process must take place in each location. Surely no place in some space that is enclosed within itself with [spatially] constant curvature can somehow be EXCEPTIONAL, so that anything can happen in it differently than in other places? That is inherent in that model.
I am still looking for a suitable English word that would describe it better. There can be no “flatulence“, no smoke is produced, no moisture supplied to make it “swell“, and no chemical reaction necessary for “effervescence” is produced. And yet, in order for the word to continue to be easily used, it should be easily translatable into foreign languages, easy to remember, and at the same time somehow convey that this kind of expansion is just a little different from the name expansion used so far.
I apologize for choosing an easy-to-remember name for such a process (perhaps with a bit of humor, 😀) ECSTASY [CZ original: EXTÁZE, NL:extase]. In Czech, it is not far from expansion [CZ original: expanze]. And if it should meet with a lot of resistance, I will apologize again and withdraw it.
20200901 >
< 20200817
The recognition of the “expansion” of space in physics required that, by backward extrapolation, we necessarily arrive at the “beginning” of such an expansion, which we call the Big Bang. A kind of singular point and singular moment where and when it all started “from nothing”. Therefore, if we look into the past, then we must also come across the end of our view, or rather the beginning, when it all began. Perpetum mobile or Perpetual motion is excluded. That’s what physics teaches us. And now all of a sudden so much energy out of nothing, that would be a blessedly big exception, wouldn’t it? (Something like we know that stealing a little money is also something completely different than stealing the whole bank, 😀).
20200817 >
< 20200917
But how can we imagine such a process, the same at every point? So that we can have at least some tangible IDEA of such an observed moving away, I would like to offer a suggestive image of a SUBSTITUTIVE CIRCLE as a Circular Dance [2NKjKT_EN]:
In the left part, we can see schematically as if you, or I, were dancing in a circle next to the brown-eyed Eve and the blue-eyed Adam (with an apology: since I am a man, I chose a more attractive place for me closer to Eve than Adam 😀) all in a red suit.
On the right part, other blue-clad dancers join the dance spatially evenly. It is easy to see from the sketch that Adam will move away from us faster than Eve (and we will also move away from Adam faster than Eve). Or to put it another way: The more distant dancers will automatically move away from us faster than the closer ones, even if their position angle φ on the circle has not changed.
The radius R of the circle is also marked on the left side, as well as how the angle φ is measured from us. On the right side, the increase in the radius of the circle is also marked, i.e. the expansion of the SUBSTITUTIVE CIRCLE. If the rate of expansion dR/dt is denoted by the symbol ΔV0, then the observed rate of receding along the arc has the magnitude ΔV0·φ.
20200917 >
< 20181202 The expanding circle of dancers in our image is reminiscent of Hawking´s IDEA, presented in a popular science program1 , where the expansion of the Universe was simplified from 3D to 2D, as if created by the mutual “pushing” of objects into space.
The skaters on the ice surface were lined up behind each other in the shape of the three-pointed star of the Mercedes brand, leaning on each other and holding some kind of airbags between them. On command, the airbags began to inflate at the same time, so that by the expansion of the airbags, they began to push each other away, in such a way that during the contact with each other, the skaters further away from the center obviously gained a greater and greater initial speed. Then, when the skaters lost contact with each other, they continued to move away from each other by inertia alone. This is how the IDEA of the universe, which was created by an explosion called the Big Bang, became popular.
Skaters resemble our Circular Dance, but they are not the same. The movement of the skaters after the end of the airbag function is considered as inertia, whereas in the circular dance, the addition of dancers to each place continues.
20181202 >
1 This IDEA of Stephen Hawking is popularly and scientifically presented in the program called
“Genius by Stephen Hawking”.
< 20210601
There, the expansion of space was perceived as an immediate activity that ended with an explosion, and further expansion continues only through the inertia of all objects that were set in motion by the explosion, and the farther from the center of the explosion, the faster. That is, not as some ongoing addition of dancers to the SUBSTITUTIVE CIRCLE, which they represent here, and which expands smoothly and evenly with the passage of time. 20210601 >
< 20200817
But our model offers something else: If in our expression of the receding velocity ΔV= ΔV0·φ the quantity ΔV0 is non-zero (ΔV0 >0), then with increasing φ the observed receding velocity will grow indefinitely. And for a sufficient distance φ from the observer, the observed speed of retreat will reach the limiting size ΔV0= c, which I called the LIGHT BARRIER 2 . I chose the name based on the “Sound Barrier”, which has proven itself in aviation, for example.
20200817 >
Professor Bicak from the Charles University in Prague pointed out to me that what I call the LIGHT BARRIER could probably best be called the “cosmological horizon” in physics. I thank him for this notice.
< 20200807
According to https://en.wikipedia.org/wiki/Cosmological_horizon, a Cosmological horizon is a measure of the distance from which one could possibly retrieve information. This observable constraint is due to various properties of general relativity, the expanding universe, and the physics of Big Bang cosmology. Cosmological horizons set the size and scale of the observable universe. This article further explains a number of these horizons (1 Particle horizon, 2 Hubble horizon, 3 Event horizon, 4 Future horizon, 5 Practical horizons).
But how does this measure of the observable Universe relate to the IDEA of the size of the Universe in contemporary cosmology? In search of an answer,
2 < 20210520 I thank Professor Krizek from the Mathematical Institute of the Academy of Sciences of the Czech Republic for pointing out how he himself had already come across a calculation that considered a speed of retreat beyond the “horizon of the universe” greater than the speed of light c. Even a speed exceeding by a factor of ten! However, the presented model does not exclude the IDEA of observing movement through a closed space along the SUBSTITUTIVE CIRCLE multiple times repeatedly, and thus the speed of retreat increasing indefinitely. So after the first orbit, the observed velocity of retreat comes out as ∆V= 2π·∆V0, and each subsequent orbit adds a 2π·∆V0increase to the velocity. Then it would be possible, at least theoretically, to consider a speed of, say, 10·c. 20210520 >
I opened the article https://en.wikipedia.org/wiki/Hubble_volume. (I must point out in advance that by opening any article on cosmology one can see the enormous amount of work that has been done in it, and how many of our brilliant predecessors have participated in its research. Therefore, it is perhaps not surprising that any layman should lose track, what can cosmology even mean to him.)
The presented visualization of the entire observable Universe is interesting:
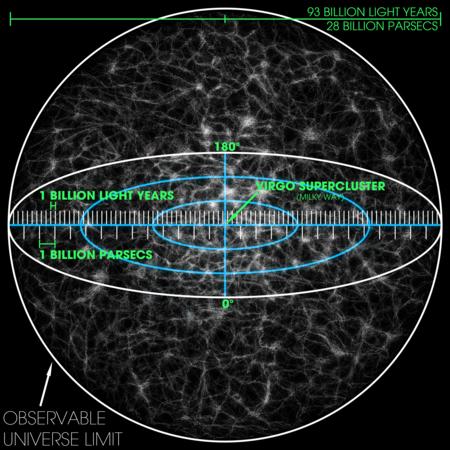
With description: Visualization of the whole observable universe. The scale is such that the fine grains represent collections of large numbers of “superclusters”. The “Virgo Supercluster“—home of Milky Way—is marked at the center, but is too small to be seen.
Since we, as observers, would observe the homogenous Universe equally deep on all sides, our position, our Earth, our Milky Way will of course be drawn in the center of the visualization. And what I call the LIGHT BARRIER, and here is called the Limit of Observable Universe, is shown here as an enveloping sphere. The same visualization is also presented at https://en.wikipedia.org/wiki/Observable_universe, specifying that the observable universe is a ball-shaped region of the universe comprising all matter that can be observed from Earth or its space-based telescopes and exploratory probes at the present time, because the electromagnetic radiation from these objects has had time to reach the Solar System and Earth since the beginning of the cosmological expansion. And data such as its diameter D=2R≈8,8·1026m, and volume V=π·R3 ·4/3≈3,6·1080m3 are added to the enveloping sphere.
20200807 >
< 20210112
But this would mean that the propagation of light to the observer in a straight line is considered here. As if the light came to us not along an arc but along a straight line. Such a straight line is used here as the radius R to determine the volume of the observable Universe as the volume of a sphere! That would not respect Einstein’s IDEA that the Universe should be considered a curved and self-contained space where light must travel to the observer along an arc? Does modern cosmology not respect this IDEA of Einstein?
If we observe everything along an arc in a curved space, and along a SUBSTITUTIVE CIRCLE in a space with constant curvature, then we spatially reach the place of the observer at a distance corresponding to the central angle of 2π (360°). And further beyond it, we would begin to observe everything again, as if in the “second round”.
20210112 >
=================================================
2NdV.2_EN Looking into Universe. 2
A. INTRODUCTION TO PART TWO
B. STARTING POINT
C. EXPANSION OF SPACE
D. IMPLICATION ON OUR OBSERVATIONS
E. OBSERVATION ALONG THE ARC
F. GRAVITY DEFICIT
< 20210113
But to describe such implications, I need to clarify a few general things first, so that I have any chance of being understood and thus prevent an avalanche of protests from my advisers/opponents. Why does physics resist limiting our observation? I myself see the root cause in the convulsive effort to maintain objectivity in physics at all costs.
Apparently what happened was that we humans were pushed off the stage of physics and pushed into the auditorium. Yes, we can observe physics, and therefore the Universe, but only from the outside. We were “kicked” out of the Universe, and that’s exactly what I can’t come to terms with for the rest of my life. We forbade ourselves that people could threaten us somehow subjectively in physics. (And perhaps rightfully so, that they will start obstructing us even here, 😀.)
However, our exile will accompany us in all the descriptions of my expeditions. Even in basic forms, such as here: How in what we think of as objective 3D space can we ever make each other’s UNIQUE subjective 2D observations of what we call objective reality? Or conversely: How can we even be able to create an IDEA of an objective 3D space from our individual subjective 2D observations? How could this be possible, when everything is moving away from every place by being pushed in all directions into the distance and also into the past, i.e. from the place where we are?
So, for example, from Adam, as in the picture OBSERVATION BUBBLE in space 2 [2BPvp2_EN] that I will present below, everything should be moving away from him into the distance and past, while Eve, who observes everything from a perpendicular direction, for example, does not observe any movement from Adam. She observes nothing at all. And also conversely, Adam observes nothing of the receding of everything into the distance and past from Eve. How is it that in such a space that runs away from us in all directions, we can even spot any 3D geometrical shapes with [mathematically] absolute precision?
< 20210115
But there is nothing to be surprised about. Since in our model the observed velocity of retreat is ΔV= ΔV0 ·φ, then mathematically, for an infinitely small dφ, an infinitely small velocity of retreat also results dΔV=ΔV0 ·dφ. And physically, for the immeasurably small curvature of space dφ ≈ 0, the speed of retreat from us must also be unobservable small dΔV ≈ 0 (all geometric shapes become absolutely exact for the limit z= R•φ when φ → 0). In other words, in our immediate surroundings, where the curvature of space is not yet observable, what I call ECSTASY cannot even be observable either.
20210115 >
But lest anyone think that the consequence I am about to mention was just some isolated idea the morning after a night´s wild dream, it is not, on the contrary. I’ve been looking for it for years, and diligently.
As an example, I will cite weeks of intensive collaboration with Dr. Josef Kajfosz, a scientist from the Institute of Nuclear Physics in Krakow, on one detail, as a result of his expert article “On the alternative interpretation of special relativity”.
First of all, I must thank him for his patience in the intensive consultation and the effort he put into our cooperation. But working with Kajfosz was worth it. Although we actually ended up “crashing” when my colleague suggested ending further discussion, because we had reached a bulletproof, immovable “wall” in physics called the Twin Paradox. And I just cheered at the same moment, because I finally realized that we had hit the same wall, but both from opposite sides of each other (!!!!). This helped me realize the nature of the wall so much that I compiled a separate study for myself from my notes called Satellite Observations and the Twin Paradox 20181025 {2PSTP_EN} in an attempt to understand it properly.
Twin Paradox [https://en.wikipedia.org/wiki/Twin_paradox], as what it is about, I will describe it in a popular way, for example: Imagine that blue-eyed Adam would shoot brown-eyed Eve, not to the Moon (😀), but much further and faster, so that Eve would make a closed path through the Universe and return to us undamaged. And while Adam was still on Earth, our Eve traveled to a number of other places that are perceived in physics as certain reference systems [EN: inertial frames. Kajfosz´s terminology: State of Inertial Motion (SIM)] and in which, according to the current accepted concept, the passage of time has slowed down in them compared to the passage of time on Earth, because they are in motion relative to the Earth. But this means that Eve will return to Adam younger than he is! Conversely, if Eve remained in one of those visited frames of reference and it was Adam who flew away from her to Earth and then returned to her, traveling the same closed path that she did, then it would be Adam who would be younger than her! However, the normal brain does not “take” this, hence the name Paradox.
Be aware, however, that in physics this is based on a certain physical concept, a certain set of Postulates as it is called, which we have worked on at the given moment through the gigantic efforts of a large number of genius predecessors.
And using the mathematical tools developed and left for us by countless genius predecessors, we can move from one concept to another, even if its implications sometimes don’t work out for us.
In addition to all this, remember that our mathematical tools are so blessed that we can rely on them day and night. They link the two concepts to us so tightly bound, with such inherent certainty, that EITHER we must accept them both OR we must reject them both! This is ensured by the fact that the basis of all our mathematical tools is actually addition, in which I also include multiplication, as repeated addition3.
< 20210322
I’ve already heard voices warning me that I’m using terms like “Twin Paradox” and “frames of reference” here without explaining how it actually relates to the “Looking into Universe” under investigation. This forced me to develop these follow-up compilations of my notes, that is, separate stages of Goulliver’s journey into the empire of the giants, into the macro world, called “Looking into Universe“.
20210322 >
3 <20210113 But beware: Only the kind of repeated addition that we can imagine, for example, as counting floor tiles in a rectangular room. After all, there we can start adding all the tiles in a row from one corner along one wall, and then repeatedly continue through the adjacent rows. Or repeatedly add up all the tiles in each column along the other wall.
This is, of course, different from the repeated counting of the votes of, for example, the US presidential election, when the repeated counting should lead to the same total of electoral votes, provided that they were not manipulated in any way in between. And this should lead to the legal election of the president with the accuracy of maybe one vote, provided, however, that all votes were obtained absolutely legally and also counted legally.
I will return to such situations in my articles on psychology, where I will hold up a mirror for us to realize the consequences of our actions. Fulfilling the above prerequisites can be very difficult if there are huge personal SELF-INTERESTS involved. And I will add to them SHARED INTERESTS, where we participate in the interests of a group of people who somehow cooperate, or collaborate, or at least identify with some group (-something like when we start to identifying with Republicans, for example, we stop identifying with the Democrats, and vice versa-) 20210113 >
And now I will tell you the consequence for which we were preparing everything. 20210113 >
< 20200114
We have prepared it to try to continue now, I hope successfully. So in mathematics, which rests in its foundations on the certainty of addition, 1+1=2 must be absolute truth (already because we mutually agreed on it 😀).
But then at the same time it must be true that 2-1=1! This results from one Boundary condition of our CONSCIOUS THINKING in my terminology called, for example, “EITHER/OR“. And this causes us to either accept 1+1=2 and at the same time 2-1=1, or we have to reject both at the same time. Corresponding consequences are accepted or excluded more easily in mathematics, but in physics it can be considerably more difficult.
So now to the point: The Twin Paradox arose in physics in parallel with two different views. One according to the IDEAS created for us by Albert Einstein, which excludes the existence of any EXCEPTIONAL frame of reference in the Universe. All systems must be equal to each other, none must be EXCEPTIONAL.
And the other view according to the IDEAS made for us by Hendrik Lorentz, in which it is required that there should be at least one UNIQUE frame of reference for us in the Universe in that it would be possible to relate to it our IDEA of relativity.
And precisely in our described IMAGINATION, in our model, we actually already managed to separate the local system in which each of us subjectively looks into the Universe (see, for example, the already presented picture SPACE 4D [2P4D_EN]) from the system of the entire objective curved space with constant curvature.
20200114 >
< 20210113
I will try to make it more visible with the help of an image that I derived from the original image showing how the brown-eyed Eve and the blue-eyed Adam observe the same object, perhaps a jewel, as if at the common point of their OBSERVATION BUBBLES, and which I called OBSERVATION BUBBLE in space 2 [2BPvp2_EN]:
I added to the picture how for each observer the observation is UNIQUE according to Lorenz, but at the same time none of them are EXCEPTIONAL according to Einstein. We actually proved both of them right. But what did we achieve? Did we eliminate the Twin Paradox? No, we didn’t create it at all.
20210113 >
Am I the only one who somehow noticed such consequences of such a model? Consequences if we consider the Universe as a closed curved space? Or am I the one who really went crazy? I always remember a joke I once heard: “Grandma and grandfather are driving on the highway. Grandma turns on the radio, where they announce: Attention, we have a report that there is one car going in the opposite direction on the highway between places “A” and “B”. And the grandfather said: How come, one car, all cars! ” 😀.
< 20201008
We have shown that the speed of retreat observed in the Universe is automatically a direct consequence of the increasing distance of the observed objects from us in our model. The receding speed is represented by the increasing angle φ, but only when ΔV0 is not equal to zero. If ΔV0=0, then there would be no increase in distance.
In other words, ΔV0 = dR/dt is the speed of ECSTASY, which we must take to be non-zero and the same at every point of the observed space with constant curvature. Then K=ΔV0 / c = Constant > 0 applies spatially. That is, a dimensionless constant, where c denotes the speed of propagation through space, for example of light (or electromagnetic waves in general), gravitational disturbances, changes in the distribution of energy in space, etc., as the last constant, when modern physics has already taken away Newton’s unchanging passage of time and the unchanging dimensions of space.
< 20210310
In order to avoid repeatedly enumerating what all in the current concept of physics propagates at that speed c, without omitting some others, I will therefore introduce the more general name INFORMATION for them. I choose this term because, whether something is spread by electromagnetic waves or gravitational disturbance, for us it is still just information about something that we observe moving away from us in our space-time into the distance and at the same time into the past. I hope I can find understanding in that too. 20210310 >
I first proposed to call this dimensionless constant K = ΔV0 / c the Cosmological Constant. But I didn’t succeed with that with Professor Bicak. And I even found out later that this name is already used in physics [https://en.wikipedia.org/wiki/Cosmological_constant], so it would only lead to more confusion. But it doesn’t really matter what we call the constant, but it should be called something so that we can refer to it simply and unambiguously.
< 20201008 Image Our 1st Postulate [2n1p_EN] summarizes the constant K:
I call it a postulate because it mathematically describes to us the same thing that could geometrically represent a model of a closed curved space with constant curvature in which we observe how all objects move away from us. That IDEA, that model, requires that constant. Both are the same thing, just written differently. So we EITHER accept both OR we must reject both. We EITHER accept both the model and the constant, OR we reject both.
But I believe that with this pair of IDEAS (which I call INTERCHANGEABLE IDEAS) we are not adding anything to Einstein’s IDEA, nor are we taking anything away from it?
20201008 >
Now I take the liberty of writing down my other “inferred” observations and consequences, which I think could result from the consequences just described. I am prepared to fail with them to all experts in cosmology or other physical sciences, so I have no choice but to apologize if I spoil their mood or otherwise burden them with thinking about them.
=================================================
2NdV.2_EN Looking into Universe. 2
A. INTRODUCTION TO PART TWO
B. STARTING POINT
C. EXPANSION OF SPACE
D. IMPLICATION ON OUR OBSERVATIONS
E. OBSERVATION ALONG THE ARC
F. GRAVITY DEFICIT
< 20201013
Our IDEA does not require the assumption of some creation of the space of the Universe from nothing. And the horizon of our observation is modeled as the limit of the observed speed of objects moving away from us ΔV=c, which I call the LIGHT BARRIER. That limit results as a consequence of the natural increase in the observed speed ΔV=ΔV0·φ with the increase of φ, and beyond which limit we no longer observe anything.
20201013 >
<20201020
It was Stephen Hawking who, with his IDEAS, drew my attention to the limitations created by describing the Universe “classically” as some kind of open space [in Cartesian x-y-z coordinates]. Later I realized the advantage of taking the Universe as a closed space [for the observer to describe it in spherical coordinates r(≡z=c•t)-φ-ψ centered at the observer’s location].
Fortunately, we do not create any damage to objectivity with our model: the physics remains the same for any point of observation, which we can freely change in our IDEA of the Universe.
And as a bonus, the spherical system of observation becomes singular, UNIQUE for each observer, so our model also fits Lorentz´s IDEA without interfering with objective physics.
We may even congratulate ourselves because this model did not give the opportunity for the “Twin Paradox” to develop.
And in addition, we began to respect the fact that Richard Feynman draws our attention to. No two observers can ever simultaneously observe anything from the same observation point. Brown-eyed Eve and blue-eyed Adam can lovingly lay forehead to forehead, or cheek to cheek, but no more. They would have to take turns observing from the same point.
I probably won’t get away with everything here. But ok, let someone disprove it and offer a better IDEA, a better model. I am ready to thank him for that.
“Our 2nd Postulate” (Our 2nd Postulate [2n2p_EN]) means, however, that in the Universe as a closed space, in which the observed objects seem to run away from us in all directions at a speed of ΔV, the model adds “something” to the space. And that addition is continuous, uniform and equally fast at all points. If ΔV0 were a constant speed not only spatially, but even temporally, then we would take the expansion of the SUBSTITUTIVE CIRCLES as stationary, dR/dt=constant, i.e. d2R/dt2=0.
And it is the search for that “something” that is added to our space everywhere that will lead us to the descriptions of my two Goulliver journeys to the world of dwarfs, i.e. expeditions to the micro world, to which I also want to invite you. We will look for some kind of bridge between the macro world and the micro world to work towards the belief that there is none. There is only one Universe and not two. We will see that the macro world and the micro world represent the same Universe, only observed from a different side. However, these expeditions cannot be done without thorough preparation, which is necessary for such trips. Before that, all we have to do is describe the foundation stones on which our search will stand.
20201020 >
< 20170106
Let us realize that until now we have considered ideal [mathematical] spaces, i.e. spaces that are infinitely thin. Since one of the conditions (Psychological Boundary Conditions, {3pop_EN}) of our CONSCIOUS THINKING, which we can label as “either ∂ or ∆“, does not allow us to divide the IDEA of something we consider concrete and real into something infinitely small (“∂ “), i.e. the space of the Universe, to something infinitely thin4. I popularly try to explain this fact in the article Mathematics and Physics {0mf_EN}, in which I draw the dividing line between mathematics and physics.
Therefore, we will extend our IDEA to a space of finite thickness (“∆“) by introducing the concept of “quantum of lengths” LC, as I describe in the article Quantum of space, time and energy {2kpce_EN}. What quantum sizes and to what IDEA of space this leads to, I am working on in the article called Quantum DOUBLE-EXCHANGE {2KDV_EN}.
As I have already pointed out, the real space of the Universe cannot have a constant curvature, because the curvature of space is caused by gravitational effects, and these are unevenly distributed in the Universe. I compiled some notes on this topic into a separate study, which I called Star Observation {2ph_EN}. There we will also show some of the consequences of local differences in the curvature of space, which deform our SUBSTITUTIVE CIRCLES into curves of variable curvature.
20170106 >
< 20210204
Without entering into a discussion about the passage of time with my description here, I am trying to do that elsewhere, I need to rely on the following here. As I point out elsewhere:
“We invented time to understand CHANGES”.
Basically, the passage of time is just a fixed sequence of CHANGES. Popularly speaking, if we arrange the CHANGES one after the other in a fixed order and number them, for example, as 1-2-3-4…, then observing from any place the order of the sequence of CHANGES will not change. By observing from nowhere, the sequence does not change for us, for example to the sequence 1-3-2-4…. Although in observation from a specific place, we can observe the sequence of such CHANGES scrambled.
How time passes at a distance from us, or even how time passed in the past, is an academic question. We are only convinced that he somehow ran (that some CHANGES must have taken place in the distance and in the past).
4 < 20170106 A circle in mathematics can be understood as infinitely thin. But the drawn circle will lose this property, and it will no longer be infinitely thin. In mathematics, the surface of a sphere can be considered infinitely thin. If we create a sphere by blowing up a soap bubble, for example, such a property is lost. 20170106 >
Let us, at least for a moment, mark the passage of time in some place observed by us in the distance and at the same time in the past as τ. How it is related to Einstein’s model for the space of the Universe, as a closed space with constant curvature, we will show in two simple cases:
(I) In the first case, we will consider the retreat of objects observed in a space in which the radius of curvature R is a spatial and time constant. Then only the angle φ of the arc between the observed moving objects (or between them and us, observers) can change with time (increase). Moving objects on the surface of the (Earth-) sphere would be observed in the same way, as an example in a space one dimension smaller.
In such a curved space, we would still understand the distance from us along the arc as z=R•φ. And with the CHANGE in time, during which the distances from us to the observed object increase, the speed of the retreat will be dz/dt= R·dφ/dτ·dτ/dt. Here t denotes the reference passage of time in our immediate surroundings, i.e. in our simultaneity, which we call the present. And to simplify, if we consider the passage of time τ and t as the same (dτ /dt=1), then the speed of retreat would be dz/dt= R·dφ/dt.
But we observe such a CHANGE through light that travels to us at speed c. And we can no longer distinguish whether the light that brings us information about the CHANGE came to us in an arc or in a straight line. This led to IDEA, which relates the distance and age of observed objects by the relation z=c•t (or dz/dt=c). So, for example, we observe an object a million light years away in the state it had a million years ago. And this applies not only to all distant observed objects, but also to mutual differences in distances and ages of
objects.
(II) In the second case, we will consider the moving away of motionless objects carried away by the ECSTASY of the expanding space at a speed ΔV0 that is spatially and temporally constant. Just like fixed objects that would move away from each other on the surface of a uniformly inflating (Earth-) sphere, again as an example in a space one dimension smaller.
The objects would stay in the same place, so φ would remain constant for them. Only objects would drift with expanding space. For the course of time τ and t the same (dτ/dt=1), increasing the radius of curvature dR/dt = ΔV0 would cause the increase of mutual distances Δz=R•Δφ between objects to appear to us as if at a rate of dz/dt= dR/dt·Δφ= ΔV0 ·Δφ. It is important to realize that even for the expansion of curved space at a constant speed ΔV0, the observed distance from us along the arc z=R•φ and also the observed speed of retreat ΔV= ΔV0•φ will increase with increasing φ.
And that would still fit our observation that Edwin Hubble brought to our attention. In non-curved space, it also appears to us that the observed speed of retreat increases with increasing distance from us, but the reason is sought in the expansion of space with a speed that increases with increasing distance from the observer.
So in both cases we observe an ever-accelerating receding with increasing distance from us. The effect in non-curved space is explained as if we are observing objects that are actually moving away at an ever-accelerating speed. Whereas in curved space we model the same effect only as the drifting of objects in space that expands at a constant speed.
I consider this to be a significant difference and perhaps the reason why we
have what I will call a GRAVITY DEFICIT below. I will try to present it even
more plastically using a sketch of the AGE and SIZE of observable
Universe [2VVpV_EN]:
Let’s imagine that the brown-eyed Eve and the blue-eyed Adam, as our representatives in observation, observe objects for us in the distance and in the past. Eve focuses on her observation being “classical” along a straight line, and Adam along an arc. And it does not matter whether Adam explains that the light traveled to him in an arc in some non-curved space, or that it traveled straight to him in some curved space, for they are but two INTERCHANGEABLE IDEAS which lead to one and the same result, to his observation. They can both look in different directions, and not just as here, in opposite directions, which I choose for the simplicity of the sketch. But they will still see more distant objects as older, since the information about the objects did not travel to them at an infinitely large speed, but only at a finitely large speed of light c.
So in their IMAGINATION they can perceive with their CONSCIOUS THINKING either the age of the objects t or their distance z, bound by the relationship z=c·t. And if they add to their IDEAS the interpretation of the red shift of light as the expansion of the Universe, by which the more distant objects are moving away from them at a speed that increases with the distance from them, then they will necessarily come to the conclusion that the
information that spreads to them cannot be from places further than some limit distance. Because then the speed of objects moving away would exceed the speed of light c.
This limiting distance is called in physics the Horizon of Universe HV. So it is the distance to the limit of the observable Universe from the place of the observer. From even more distant places, which could be moving away from us faster than c, light would no longer reach us. It would propagate towards us at a speed c in an environment that would move away from us faster than c.
The fact that I call that limit a LIGHT BARRIER does not change things. It only happened because we came to it with a different reasoning. We will therefore mark the distance to this barrier from the observer’s place as the LIGHT BARRIER of Universe SBV, so then SBV= HV.
Since in our IMAGINATION the light flew along the entire path to us at speed c, these distances correspond to a certain interval of the passage of time in our place of the observer, which we will call the AGE of UNIVERSE VV. So then HV≡ SBV= c·VV.
In our description of the model, according to Einstein’s IDEA, as a selfcontained space with a spatially constant curvature, we can however interpret the distance from us as the distance along a circular arc z= R•φ, in which R again denotes the radius of the circular arc, and φ denotes the corresponding angle of the length of the arc measured in the direction from us observers to the observed objects in the arc measure.
Let’s add to the IMAGE the interpretation that the observed red shift of light is a consequence of the ECSTASY of the Universe, which carries space-time at a spatially constant speed ΔV0= dR/dt from every place to all sides, i.e. from all possible places of our observation. Adam, observing ECSTASY along the arc, sees the increasing speed of retreat as dz/dt= dR/dt·φ=ΔV0·φ= ΔV.
In the IDEA of the ECSTASY of the Universe, we can then call the Observable SIZE of UNIVERSE RPV as the distance to which the space was carried away at the velocity of ECSTASY ΔV0, from us in all directions, during the AGE of UNIVERSE, during the time interval VV. This gives us RPV= ΔV0 ·VV.
Since we call the inverse value of a time interval the repetition frequency of that interval, for completeness we can similarly call the inverse value of the AGE of UNIVERSE VV as the FREQUENCY of UNIVERSE fV, where fV= 1/VV= ΔV0 /RPV. It determines how frequently the ECSTASY of the Universe will carry the space-time from every place in the Universe up to a distance equal to the SIZE of Observable UNIVERSE RPV and into the past equal to the AGE of UNIVERSE VV.
In order to express the drift speed of ECSTASY ΔV0 with a dimensionless constant, we introduced the quantity K= ΔV0 /c, where c is the speed of light with the meaning at which speed the INFORMATION about ECSTASY returns to us from every place in the Universe. Then K denotes the magnitude of ΔV0 as a fraction of the velocity c.
20210204 >
=================================================
2NdV.2_EN Looking into Universe. 2
A. INTRODUCTION TO PART TWO
B. STARTING POINT
C. EXPANSION OF SPACE
D. IMPLICATION ON OUR OBSERVATIONS
E. OBSERVATION ALONG THE ARC
F. GRAVITY DEFICIT
I hesitated for a long time to add this last chapter to my compilation of notes entitled “Looking into Universe 2″ because I didn’t know how to write such an addendum. Encouraged, I decided to try to write it down somehow. But I’m not sure that my description will be enough to understand the following model validation possibilities that appear to me. In order to avoid a possible avalanche of misunderstandings, I will at least clarify my way of looking at the matter first.
< 20201013
In our IMAGINATION, we model our observation into the distance and into the past (!), which takes place along the arc of curvature z=R•φ, and we also model the observed speed of the objects moving away ΔV=ΔV0·φ. Current physics is probably based on the IDEA of looking into the distance, i.e. in the direction of “expansion”, and the IDEA of looking into the past, i.e. in the direction against “expansion”, it must ignore, does not respect it, or at least turns its back on it.
20201013 >
< 20201014
What is the consequence? Gravity between more distant [but unfortunately not older (!)] objects must then, as we expect, weaken faster. We observe distances between objects in non-curved space larger and growing faster than they are in curved space. After all, observation into the distance corresponds to observation in the direction of expansion in non-curved space, and this leads to the expectation of a faster expansion of space than the expansion of curved space. (For an observation into the past, as an observation against the direction of such expansion, it would even lead to the expected opposite of expansion, i.e. some contraction of space). The expected faster expansion of space in physics must also lead to the expectation of a faster weakening of gravity. So it leads to an expectation that is not confirmed in our observation. On the contrary, our observations may alert us as if some gravity is missing in the distant Universe. So we probably have no choice but to substitute some gravity for the missing gravity. What can we already do, using, for example, the so-called “dark matter“?
20201014 >
< 20210202
But now I have to choose a name. Either GRAVITY DEFICIT [CZ original: GRAVITAČNÍ DEFICIT], or DEFICIT of GRAVITY [CZ original: DEFICIT GRAVITACE]? Let’s face it, I’ll choose the first one.
We will roughly describe the idea of GRAVITY DEFICIT using a sketch called GRAVITY DEFICIT [2GD_EN]:
I’d rather leave the actual relationship between the observed red shift of light, i.e. the speed at which objects are moving away, and the GRAVITY DEFICIT to the experts.
A speed diagram is drawn on the sketch, where the speed of moving away is plotted on the vertical axis, and the passage of time to the past and distance on the horizontal axis:
- on the upper edge is the time of the objects moving away from us t’, and on a different scale
- on the bottom edge is the flight time of light from the objects back to us t.
We, as observers at point O, observe objects moving away from us. Both the object´s speed of receding “v” and the distance “z” (and the corresponding age z/c) are determined from the observed red shift of the incident light propagating back from the objects to us observers at speed c.
In our described model for spatially constant curvature, space expands by ECSTASY in all directions from observers at the same speed ΔV0≡ dR/dt <c, where ΔV0 is a spatial constant.
If we consider ECSTASY as a stationary process, then ΔV0 also becomes a time constant. Since for the observable Universe we have already marked its age as the AGE of UNIVERSE t=Vv, then for the drifting speed of ECSTASY ΔV0 the Observable SIZE of UNIVERSE will be RPv=ΔV0•Vv, which in the sketch corresponds to the area of the rectangle with vertices D-E-I-O.
Since the speed of retreat ΔV0 is a fraction K of the speed of light c, (K=ΔV0/c), then the time of flight of light back t will be in the same ratio shorter than the time required for objects to move away t´ (t= t´•K). In the sketch, the ratio of the areas of the rectangles D-E-I-O and D-K-N-O, or the ratio of the segments I-O and N-O, and of course also D-E and D-K, corresponds to the ratio K.
However, since we observe objects in a curved space along a circular arc, then the farthest observed object can never lie further than on the opposite side of the circle, i.e. from the observer at a distance of φ=π. Because any observed object for φ>π would actually already be observed in the opposite direction for φ<π. However, we cannot count such an object into the Universe twice, because it cannot even be in the Universe twice. In order not to include the space of the Universe in the “second round”, then the “real” SIZE of UNIVERSE comes out as Rv= R·π, which in the sketch corresponds only to the area of the C-F-I-O rectangle marked in blue.
If we simply consider the speed of retreat of objects v as linearly dependent on their age t and at the same time on their distance z= c·t (for example, for an object twice as far away and therefore twice as old, its receding speed is also doubled), then we can express the increasing speed in sketch with diagonal v= c·t/Vv, led by points O-H-J-K. This is because the time t equal to the AGE of UNIVERSE t=Vv corresponds precisely to the speed of retreat v=c. And if for the entire time Vv the light will spread towards us at a constant speed c, then Hv≡ SBv= c·Vv will be valid for the Horizon of Universe Hv and the LIGHT BARRIER of Universe SBv, corresponding to the area of the entire rectangle D-K-N-O on the sketch.
So the speed v in the sketch increases linearly with time (in the relationship v= c·t/Vv c and Vv are constants), the speed is marked with a diagonal in the sketch. And we take the receding speed ΔV0 by ECSTASY in the model of curved space as constant, marked on the sketch by the blue horizontal line E-F-G-H-I. Since the areas of the hatched triangles A-H-O and G-H-J (and therefore also of the symmetrical triangle H-I-O) are the same, the distance at points G and J will be the same for both models. That distance for the curved space model will correspond to the area of the rectangle B-G-I-O, and for the non-curved space model it will correspond to the equally large area of the triangle B-J-O.
Up to point H, the speed of retreat in the non-curved model was lagging behind, but at points G and J the distances equalized. And then for places further away from us, the distance in non-curved space will increase more and more rapidly than in curved space.
Now let’s focus only on the distances between observed objects. Distances between objects in the curved space model will be indicated by blue and underlined Δz, while in the non-curved model by black Δz. Then, for objects further away than at points G and J, the distance between objects for non-curved space is not only larger Δz>Δz, but will also grow faster and faster.
But this will cause us that for a greater distance from us, the distance between objects Δz will not only be greater, but also the expected gravity between them will be weaker than would correspond to the distance Δz in curved space, since the intensity of gravity decreases according to Newton’s IDEA with the square of the distance. And the moment the expected weakened gravity stops matching our observation, we begin to realize that we are actually missing some gravity in the distant Universe. I called this fact the GRAVITY DEFICIT.
This may have led to the expectation of some unobservable mass that supplements the missing gravity with its gravity, and which we are unable to directly observe, not even its motion and inertial effects, only its gravitational effects. And because we consider this matter invisible, it was given the name “dark matter” https://en.wikipedia.org/wiki/Dark_matter:
„Dark matter is a form of matter thought to account for approximately 85% of the matter in the universe and about a quarter of its total mass–energy density or about 2.241×10−27 kg/m3. Its presence is implied in a variety of astrophysical observations, including gravitational effects that cannot be explained by accepted theories of gravity unless more matter is present than can be seen“.
But this opens up the possibility that the described Einstein model of curved space could replace the cause of GRAVITY DEFICIT as the expected “dark matter” by the ECSTASY of space with the space constant ΔV0. In other words, the possibility that even the size of the spatial constant ΔV0 could somehow be determined from the shift of red light in such a way that the “missing” gravity is supplemented and the necessity of introducing “dark
matter” is eliminated. Of course, that would be a task and an effort for some experts, but I cannot compete with them in any way. So the second verification option is:
(2) Adjusting the model parameters until the model eliminates the GRAVITY DEFICIT.
20210202 >
< 20211116
I will try to make the problem of GRAVITY DEFICIT more visible using the image STARS and LIGHT PROPAGATION G [2phG_EN] from the first part of this file. There I show 3 sketches, but by combining them, we rework them into one, as shown in the picture Distortion of Observed Distances [2ZpV_EN]:
The figure shows how the light from the farthest light source at point “S3” propagates to us observers at point “P” along the densely marked SUBSTITUTIVE CIRCLE, so that we observe it as if it were arriving at us from the apparent position “Z3“, deflected from the join P-S3 by a maximum angle of 90°. And the light from the nearer source “S2” is observed to propagate along the lighter-drawn SUBSTITUTIVE CIRCLES, as if coming from the apparent position of “Z2” deflected, for this situation, by an angle of 45°.
But we simplify the situation by thinking of the stars “S1“, “S2” and “S3” (from sketches 1 to 3) as if they existed simultaneously. That’s why we stop the flow of time for a while and thus freeze their positions in space-time. Although, for example, the light from S2 flew to us observers at point “P” along an arc at a distance of L2=R·π/2 and from S3 at a double distance of L3=R·π (R is the radius of curvature of space), we are actually observing the star S3 in a double past than the S2 star. By freezing the passage of time, we will take their positions in space as unchanging.
From the observer at the point P, the star S2 is distant V2=R·√2 and the star S3 V3=2·R, thus their actual mutual distance marked in blue is V23=(2-√2)·R ≈0,5858·R. But we, as observers at P, observe the star S2 in its apparent position Z2 from us at a distance L2=R·π/2 in a direction 45° deflected from the link P-S2. And we observe the star S3 in its apparent position Z3 from us at a distance L3=R·π in a direction 90° deviated from the same connecting line. Their mutual angle in our observation will therefore be 45°, as marked in the figure.
According to the cosine theorem, the square of their mutual distance, observed by us, is L232=L22+L32-2·L2·L3·cos45°=R2·π2·(5/4-1/√2)≈ 5,35814·R2, and their observed distance L23≈ 2,3148·R versus the true distance V23≈0,5858·R, so L23/V23≈ 3,95. The distorted distance L23 is almost four times larger (!) than the true distance V23, and thus the corresponding mutual gravitational effect would come out, for this situation, almost sixteen times weaker (!!).
If we consider that the star S1 is close to us (L1≈V1≈0), so the influence of the curvature of space on its observation is still negligible, then we can similarly calculate the corresponding distortion of the observed L12 (=L2), and the actual V12 (=V2) distance between S1 and S2, closer to us observers, as L12≡L2= R·π/2≈ 1,5708·R and V12≡V2= R·√2≈ 1,4142·R, so L12/V12≈ 1,11. The distortion also increased the observed distance, but only slightly by about 11% compared to the true distance.
Although, just for simplicity, we have chosen the special symmetric case of observing objects from us in a straight line behind each other, and to freeze the passage of time, we limit the validity to their mutual distances significantly smaller than the radius of curvature of space, and to the speed of their changes in position in space significantly less than the speed of light, we have shown how the model predicts an amplifying effect of increasing the mutual distances of observed objects with their increasing distance from us.
If we consider such large distortions of the mutual distances of observed objects in the distant Universe, as predicted by the described model, we cannot avoid thinking about a large GRAVITY DEFICIT between them.
This could point to a hitherto misinterpreted curvature effect that may have required so-called dark matter to be introduced to compensate for the missing gravity with its gravity. That is, some invisible matter that is believed to make up approximately 85% of the matter in the Universe. That is, such a large amount that only 15% (!!!) of observable “light matter” would be left in the Universe.
In my consultations with experts in physics, I was assured that they are all convinced of the correctness of the so-called Einstein field equation (and also the corresponding Friedmann equation https://en.wikipedia.org/wiki/Friedmann_equations), which resulted from a large number of successful applications. But why did their results begin to require dark matter?
Although I myself am forced to accept that these equations correctly describe the considered situations, it is quite possible that they only correctly describe poorly modeled situations. That is, situations that do not adequately model the curvature of space?
20211116 >
Of course, that would be another unexpected situation for many people, including me. That was the reason why, after consultations with Professor Krizek, I divided the description of the first 3 consequences of my chosen model “Looking into the Universe” into two parts. Although all the consequences are reminiscent of optical distortions and I call them the first, second and third optical illusions in looking into the Universe, their eventual acceptance can take place in completely different ways.
The first optical illusion causes that we may be mistaken in thinking that we are observing a unique space object in each direction, but they may be observations of just one the same object, in different directions, grouped into a ring in the sky that increases its diameter with the distance to the observed object. This may be unexpected, but it should not cause any great personal resentment.
But the third optical illusion, which I call the GRAVITY DEFICIT, is something else. I can imagine that someone who has been searching for dark matter all his life, or much of his professional career, might not be enthusiastic to hear that it might just be some optical distortion that I cheekily call an optical illusion! That can hurt, and I wouldn’t want to hurt such a person.
< 20211112
In conclusion, we can summarize that the described model predicts what the content of the first part is and what I call “The first optical illusion of looking into the Universe”. This reminds us of “Local Gravitational Lensing“, a known consequence of strong local gravity, so we could call it as “Global Gravitational Lensing“, which could be a consequence of the weak global gravity that holds the Universe together.
But we also described two other possible optical illusions. The second one, which explains the progressively increasing red-shift of light from more distant galaxies, as an optical distortion inherently caused by observing in curved space that expands equally in all places, an effect I call the ECSTASY of space.
The third optical illusion of looking into the Universe is based on the finding that the distances between faraway objects are significantly smaller in a model of curved space enclosed in itself than in open space. It would mean that current physics may correctly calculate the observed situation but in a poorly modeled curved space, thus calculates the GRAVITY DEFICIT in the distant Universe and the need to compensate it with the so-called dark matter.
20211112 >
< 20211119
But let’s be aware that the Milky Way’s gravitational field affects such observations, which might be easier to make by someone outside the galaxy. But we live neither outside the galaxy nor in the middle of it.
The path by which the light would otherwise spread to us along the surface of the “rugball” must be additionally deformed differently in different directions. Such an influence, such a distortion, could be the smallest for the axis of the “rugball” in the direction parallel to the axis of rotation of the galaxy, or in the direction connecting our position with the center of the galaxy. The gravitational lens could be “sharpened” for us in such directions than in other directions.
Compensating for observations affected by the distortion of the Milky Way’s gravitational field could be a complex task. On the other hand, the expected effect on the observation of GRAVITY DEFICIT from inside the galaxy could be smaller. This is an observation made at a small viewing angle, so the expected mutual differences in the path of light could be smaller. 20211119 >
This is how I finished the description of the second part, the second stage of the research expedition called Looking into the Universe. In the next stages, I will present a compilation of my notes to describe further implications of using a closed-space model with constant curvature to roughly describe the space of the Universe as a whole.
In the third part, the consequences of a broader understanding of the space-time modeled in this way are presented, and in the fourth part, a comparison of the consequences of the closed and open space model is elaborated.
< 20210330
Acknowledgement
I thank all the brilliant predecessors, the authors of this work, who gave me the opportunity to try to summarize and interpret some of their results. I would also like to thank all the members of my family who put up with my writing and sometimes even contributed to its formulation.
I also thank everyone else who contributed to my writing. In addition to a number of unnamed, they are:
- Professor Jiri Bicak persistently guided my thoughts.
- Professor Michal Krizek gave me valuable information and assessment.
- RNDr Josef Kajfosz helped me clarify the Einstein – Lorentz differences.
- RNDr Jiri Kopecky CSc introduced me to him and encouraged me in writing.
- MSc Jan Kaspar and Jan Slama taught me how to express myself popularly.
- Mr. Martin Oresansky from Royalonogy converted my articles to the World Press web format.
And finally, I would also like to thank you, dear reader, for the attention you gave me by reading this second part. Thank you.
20210330 >
